
【题目】一个多面体的三视图![]() 正视图、侧视图、俯视图
正视图、侧视图、俯视图![]() 如图所示,M,N分别是
如图所示,M,N分别是![]() ,
,![]() 的中点.
的中点.
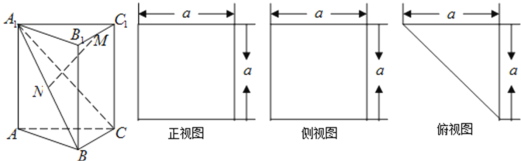
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若这个多面体的六个顶点A,B,C,![]() ,
,![]() ,
,![]() 都在同一个球面上,求这个球的体积.
都在同一个球面上,求这个球的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)根据三视图的性质,可得该几何体是直三棱柱,且![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,矩形
,矩形![]() 中对角线
中对角线![]() 的中点N就是
的中点N就是![]() 的中点.结合M是
的中点.结合M是![]() 的中点证出
的中点证出![]() ,由线面平行的判定定理,证出
,由线面平行的判定定理,证出![]() 平面
平面![]() .
.
(2)由![]() 平面
平面![]() ,得到
,得到![]() 正方形
正方形![]() 中可得
中可得![]() ,结合线面垂直判定定理,证出
,结合线面垂直判定定理,证出![]() 平面
平面![]() ,再由
,再由![]() ,可得
,可得![]() 平面
平面![]() ;
;
(3)根据三棱柱![]() 是直三棱柱,在矩形
是直三棱柱,在矩形![]() 中算出可得
中算出可得![]() ,从而得到
,从而得到![]() ,同理得
,同理得![]() ,所以点N是多面体的外接球心,得到半径
,所以点N是多面体的外接球心,得到半径![]() 由球的体积公式,即可算出该外接球的体积.
由球的体积公式,即可算出该外接球的体积.
解:由题意可知,这个几何体是直三棱柱,且![]() ,
,![]() ,
,
(1)连接![]() ,
,![]() ,由直三棱柱的性质,得
,由直三棱柱的性质,得![]() 平面
平面![]() ,
,
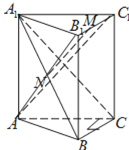
![]() ,可得四边形
,可得四边形![]() 为矩形.
为矩形.
由矩形的性质,得![]() 过
过![]() 的中点N.
的中点N.
在![]() 中,由中位线性质得
中,由中位线性质得![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
(2)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
在正方形![]() 中,可得
中,可得![]()
又![]() ,
,![]() 平面
平面![]()
又![]() ,
,![]() 平面
平面![]()
(3)![]() 多面体为直三棱柱,
多面体为直三棱柱,
![]() 矩形
矩形![]() 中,
中,![]()
可得![]() ,
,
![]() 是直角三角形斜边的中线,
是直角三角形斜边的中线,![]()
同理可得![]()
![]() 是这个多面体的外接球的球心,半径
是这个多面体的外接球的球心,半径![]() ,
,
![]() 外接球的体积
外接球的体积![]()


科目:高中数学 来源: 题型:
【题目】四面体ABCD的每个顶点都在球O的表面上,AB是球O的一条直径,且AC=2,BC=4,现有下面四个结论:
①球O的表面积为20π;②AC上存在一点M,使得AD∥BM;
③若AD=3,则BD=4;④四面体ABCD体积的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②B.②④C.①④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商品的销售价格与销售量密切相关,为更精准地为商品确定最终售价,商家对商品A按以下单价进行试售,得到部分的数据如下:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求销量![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每件商品![]() 的成本是
的成本是![]() 元,为了获得最大利润,商品
元,为了获得最大利润,商品![]() 的单价应定为多少元?(结果保留整数)
的单价应定为多少元?(结果保留整数)
参考数据:![]() ,
,![]() ,
,![]() )(参考公式:
)(参考公式: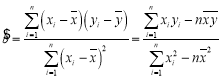 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
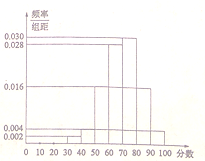
【题目】2016年某市政府出台了“2020年创建全国文明城市(简称创文)”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分, ![]() 内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
(1)求被调查者满意或非常满意该项目的频率;
(2)若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
(3)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记![]() 为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是我国南北朝时代的伟大科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”,称为祖暅原理.意思是底面处于同一平面上的两个同高的几何体,若在等高处的截面面积始终相等,则它们的体积相等.利用这个原理求半球O的体积时,需要构造一个几何体,该几何体的三视图如图所示,则该几何体的体积为_____,表面积为_____.
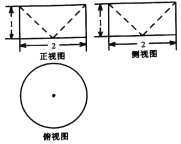
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,点
,点![]() 是棱
是棱![]() 的中点,设直线
的中点,设直线![]() 为
为![]() ,直线
,直线![]() 为
为![]() .对于下列两个命题:①过点
.对于下列两个命题:①过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都相交;②过点
都相交;②过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都成
都成![]() 角.以下判断正确的是( )
角.以下判断正确的是( )
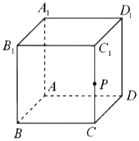
A.①为真命题,②为真命题B.①为真命题,②为假命题
C.①为假命题,②为真命题D.①为假命题,②为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学成就甚大,在世界科技史上占有重要的地位.“算经十书”是汉、唐千余年间陆续出现的10部数学著作,包括《周髀算经》、《九章算术》、……、《缀术》等,它们曾经是隋唐时期国子监算学科的教科书.某中学图书馆全部收藏了这10部著作,其中4部是古汉语本,6部是现代译本,若某学生要从中选择2部作为课外读物,至少有一部是现代译本的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com