
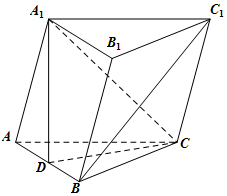
 如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点.分析 (Ⅰ)连结AC1,A1C,交于点O,连结OD,推导出OD∥BC1,由此能证明BC1∥平面A1CD.
(Ⅱ)连结A1B,推导出A1D⊥AB,DC⊥AB,由此能证明AB⊥平面A1CD.
(Ⅲ)推导出A1D⊥平面ABC,由此能求出三棱柱ABC-A1B1C1的体积.
解答 证明:(Ⅰ)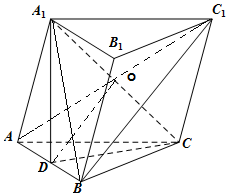 连结AC1,A1C,交于点O,连结OD,
连结AC1,A1C,交于点O,连结OD,
∵三棱柱ABC-A1B1C1中,ACC1A1是平行四边形,∴O是AC1的中点,
∵D是AB的中点,∴OD是△ABC1的中位线,∴OD∥BC1,
∵BC1?平面A1CD,OD?平面A1CD,
∴BC1∥平面A1CD.
(Ⅱ)连结A1B,
∵三棱柱ABC-A1B1C1中,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点,
∴△ABA1是等边三角形,∴A1D⊥AB,DC⊥AB,
∵A1D∩CD=D,∴AB⊥平面A1CD.
解:(Ⅲ)∵AB=AC=2,${A_1}C=\sqrt{6}$,AC=BC,AB=AA1,∠A1AB=60°,D是AB的中点,
∴AD=CD=$\sqrt{4-1}=\sqrt{3}$,∴AD2+CD2=A1C2,
∴A1D⊥CD,又A1D⊥AB,AB∩CD=D,
∴A1D⊥平面ABC,
∴三棱柱ABC-A1B1C1的体积:
V=S△ABC•A1D=$\frac{1}{2}×AB×CD×{A}_{1}D$=$\frac{1}{2}×2×\sqrt{3}×\sqrt{3}$=3.
点评 本题考查线面平行、线面垂直的证明,考查三棱柱的体积的求法,是中档题,解题时要 认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
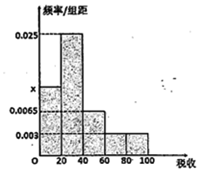 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 科研费用支出(xi) | 利润(yi) |
| 2011 2012 2013 2014 2015 2016 | 5 11 4 5 3 2 | 31 40 30 34 25 20 |
| 合计 | 30 | 180 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com