
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨< ![]() )的部分图象如图所示,则f(x)的解析式为( )
)的部分图象如图所示,则f(x)的解析式为( ) 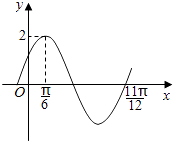
A.f(x)=2sin(x+ ![]() )
)
B.f(x)=2sin(2x+ ![]() )
)
C.f(x)=2sin(2x﹣ ![]() )
)
D.f(x)=2sin(4x﹣ ![]() )
)
科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆![]() 的焦距为
的焦距为 ![]() ,直线
,直线![]() 被椭圆
被椭圆 ![]() 截得的弦长为
截得的弦长为![]() .
.

(1)求椭圆 ![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆 ![]() 上的动点,过原点
上的动点,过原点![]() 引两条射线
引两条射线![]() 与圆
与圆![]() 分别相切,且
分别相切,且![]() 的斜率
的斜率![]() 存在. ①试问
存在. ①试问 ![]() 是否为定值?若是,求出该定值,若不是,说明理由;
是否为定值?若是,求出该定值,若不是,说明理由;
②若射线![]() 与椭圆
与椭圆 ![]() 分别交于点
分别交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ ![]() .
.
(1)判断f(x)的奇偶性并说明理由;
(2)当a=16时,判断f(x)在x∈(0,2]上的单调性并用定义证明;
(3)试判断方程x3﹣2016x+16=0在区间(0,+∞)上解的个数并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米. 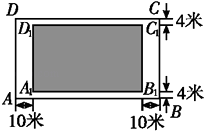
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互不相等的三个正数x1 , x2 , x3成等比数列,且点P1(logax1 , logby1)P2(logax2 , logby2),P3(logax3 , logby3)共线(a>0且a≠0,b>且b≠1)则y1 , y2 , y3成( )
A.等差数列,但不等比数列
B.等比数列而非等差数列
C.等比数列,也可能成等差数列
D.既不是等比数列,又不是等差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com