
| 4 |
| 5 |
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) |
| cosθcos(π-θ)+cos(θ-2π) |
| 2π |
| 5 |
| 2π |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
| -cosθ |
| cosθ(-cosθ-1) |
| cosθ |
| cosθ(-cosθ)+cosθ |
| 1 |
| 1+cosθ |
| 1 |
| 1-cosθ |
| 2 |
| 1-cos2θ |
| 2 | ||
(-
|
| 25 |
| 8 |


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2012年人教A版高中数学必修四1.1任意角和弧度制练习卷(二)(解析版) 题型:解答题
解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
(3)已知一扇形的周长为40cm,求它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省东莞一中高一(下)第一次月考数学试卷(解析版) 题型:解答题
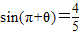 ,求
,求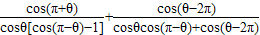 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com