
【题目】在正方体![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,
,![]() (其中
(其中![]() ),若平面
),若平面![]() 与线段
与线段![]() 的交点为
的交点为![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=![]() ,(n∈N*)
,(n∈N*)
(1)求数列{an}的通项公式an,
(2)若数列{bn}满足bn=(3n﹣1)![]() an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x+3=0,过原点的直线l与圆C有公共点.
(1)求直线l斜率k的取值范围;
(2)已知O为坐标原点,点P为圆C上的任意一点,求线段OP的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)现从上述表格中随机抽取一年数据,试估计该年城镇人均住房建筑面积达到小康生活住房标准的概率;
(2)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(3)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为![]() ,农村人均住房面积的方差为
,农村人均住房面积的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
(注:方差![]() ,其中
,其中![]() 为
为 ![]()
![]() ,……
,…… ![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() 且四个顶点构成面积为
且四个顶点构成面积为![]() 的菱形.
的菱形.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,记
两点,记![]() 中点为
中点为![]() ,坐标原点为
,坐标原点为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,当四边形
两点,当四边形![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
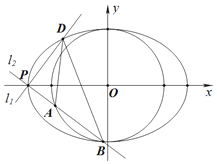
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点,![]() 的短轴是圆
的短轴是圆![]() 的直径,直线
的直径,直线![]() ,
,![]() 过点P且互相垂直,
过点P且互相垂直,![]() 交椭圆
交椭圆![]() 于另一点D,
于另一点D,![]() 交圆
交圆![]() 于A,B两点
于A,B两点
![]() Ⅰ
Ⅰ![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() Ⅱ
Ⅱ![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以椭圆![]() 的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
(1)求椭圆![]() 的方程:
的方程:
(2)若![]() 是椭圆
是椭圆![]() 上的动点,求
上的动点,求![]() 的取值范围;
的取值范围;
(3)直线![]() :
:![]() 与椭圆
与椭圆![]() 交于异于椭圆顶点的
交于异于椭圆顶点的![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() 点,直线
点,直线![]() 和直线
和直线![]() 的斜率之积为1,直线
的斜率之积为1,直线![]() 与
与![]() 轴交于点
轴交于点![]() .若直线
.若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 试判断
试判断![]() ,是否为定值,若是,求出该定值;若不是,说明理由.
,是否为定值,若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 边上的点,满足
边上的点,满足![]()
![]() (如图1).将△
(如图1).将△![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连结
成直二面角,连结![]() 、
、![]() (如图2)
(如图2)


(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com