
【题目】已知定义在![]() 上,且周期为2的函数
上,且周期为2的函数![]() 满足
满足![]() ,若函数
,若函数![]() 有3个零点,则实数
有3个零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
先作出函数f(x)的图像,再把问题转化为函数f(x)的图像和函数y=kx+3的图像有3个零点,
再对k分类讨论,数形结合分析得到k的取值范围.
先画出函数f(x)在一个周期[-1,1]上的图像,再把函数的图像按照周期左右平移得到函数f(x)在原点附近的图像,如图所示,
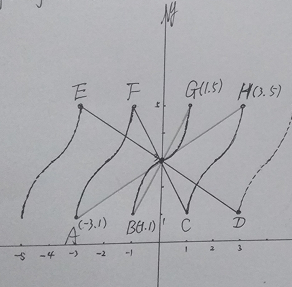
函数![]() 有3个零点等价于函数f(x)的图像和函数y=kx+3的图像有3个零点,
有3个零点等价于函数f(x)的图像和函数y=kx+3的图像有3个零点,
直线y=kx+3过定点(0,3),把直线y=kx+3绕点(0,3)旋转,
当k>0时,该直线由AH旋转到BG(不包括端点),此时它们的图像恰好有三个交点,
因为![]() ,
,
所以此时![]() .
.
当k<0时,该直线由CF旋转到DE(不包括端点),此时它们的图像恰好有三个交点,
同上可得![]() .(此处也可以由对称性得到).
.(此处也可以由对称性得到).
当k=0时,显然不成立,
故答案为:C.


科目:高中数学 来源: 题型:
【题目】某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.

(1)求![]() 的值;
的值;
(2)现从成绩高于125分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(0,+∞)上的函数f(x)满足f(![]() )=f(x1)-f(x2),且当x>1时,f(x)<0.
)=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() :
:![]() 的焦点
的焦点![]() 的直线
的直线![]() (倾斜角为锐角)交抛物线于
(倾斜角为锐角)交抛物线于![]() ,
,![]() 两点,若
两点,若![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 并延长交抛物线
并延长交抛物线![]() 于点
于点![]() ,已知
,已知![]() ,则直线
,则直线![]() 的斜率是( )
的斜率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com