
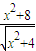 的最值时,我们可以将
的最值时,我们可以将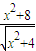 化成
化成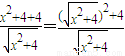 ,再将分式分解成
,再将分式分解成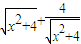 ,然后利用基本不等式求最值;借此,计算使得
,然后利用基本不等式求最值;借此,计算使得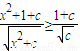 对一切实数x都成立的正实数c的范围是 .
对一切实数x都成立的正实数c的范围是 .  ,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于
,这是积为定值的两个式子的和.在x2+c=1时,即x2=-c+1≥0,它的最小值为2.此时c∈(0,1].接下来讨论当c>1时和0<c≤1的两种情况下不等式左边的最小值,再解这个最小值大于或等于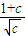 ,最后可得正实数c的范围.
,最后可得正实数c的范围.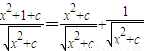
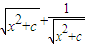
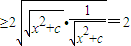
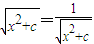 时等号成立,此时x2+c=1
时等号成立,此时x2+c=1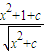 的最小值应该是x=0时的值,即
的最小值应该是x=0时的值,即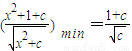
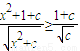 对一实数x都成立,符合题意.
对一实数x都成立,符合题意.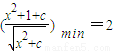
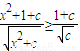 对一切实数x都成立
对一切实数x都成立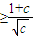 成立,可得
成立,可得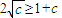 ⇒
⇒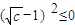 ⇒c=1
⇒c=1

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| σ | 2 |
| 1 |
| N |
| 1 |
| N |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+8 | ||
|
| x2+8 | ||
|
| x2+4+4 | ||
|
(
| ||
|
| x2+4 |
| 4 | ||
|
| x2+1+c | ||
|
| 1+c | ||
|
查看答案和解析>>
科目:高中数学 来源:2013届吉林省高二下学期期末理科数学试卷(解析版) 题型:选择题
经过对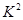 的统计量的研究,得到了若干个临界值,当
的统计量的研究,得到了若干个临界值,当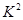 的观测值
的观测值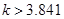 时,我们( )
时,我们( )
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A. 在错误的概率不超过0.05的前提下可认为A与B有关
B. 在错误的概率不超过0.05的前提下可认为A与B无关
C. 在错误的概率不超过0.01的前提下可认为A与B有关
D.没有充分理由说明事件A与B有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com