
已知数列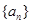 是等差数列,
是等差数列,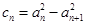 (
( ).
).
(Ⅰ)判断数列 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(Ⅱ)如果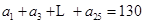 ,
, (
( 为常数),试写出数列
为常数),试写出数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,若数列 得前
得前 项和为
项和为 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使 当且仅当
当且仅当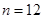 时取得最大值.若存在,求出
时取得最大值.若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅰ)数列 是等差数列;(Ⅱ)
是等差数列;(Ⅱ)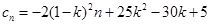 ;(Ⅲ)
;(Ⅲ)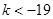 或
或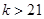 .
.
解析试题分析:(Ⅰ)等差数列的证明一般是从定义出发,注意若用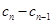 为常数,则需
为常数,则需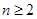 且
且 ;若用若用
;若用若用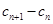 则
则 为常数,则需
为常数,则需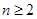 .(Ⅱ)因为
.(Ⅱ)因为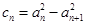 ,所以求数列
,所以求数列 的通项公式,关键是先求出等差数列
的通项公式,关键是先求出等差数列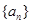 的通项公式,即求出
的通项公式,即求出 ,这样就必须建立关于
,这样就必须建立关于 的两个方程,求出
的两个方程,求出 ,显然必须从条件提供的两个等式出发去求解,注意求解的技巧;(Ⅲ)关于等差数列前
,显然必须从条件提供的两个等式出发去求解,注意求解的技巧;(Ⅲ)关于等差数列前 项和的最值问题,通常有两个思路,其一,从求和公式考虑,因为求和公式是关于
项和的最值问题,通常有两个思路,其一,从求和公式考虑,因为求和公式是关于 的二次式,可以结合二次函数知识解决问题,但要注意数列自身的特点,即
的二次式,可以结合二次函数知识解决问题,但要注意数列自身的特点,即 ;其二,从通项考虑,看何时变号.此题从通项考虑比较好.
;其二,从通项考虑,看何时变号.此题从通项考虑比较好.
试题解析:(Ⅰ)设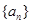 的公差为
的公差为 ,则
,则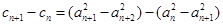

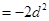
 数列
数列 是以
是以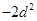 为公差的等差数列.
为公差的等差数列.
(Ⅱ)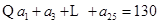

 两式相减:
两式相减: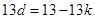
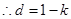
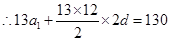 ,
,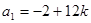
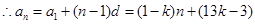

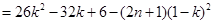
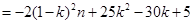
(Ⅲ)因为当且仅当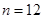 时
时 最大
最大 有
有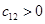 ,
,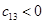 ,
,
即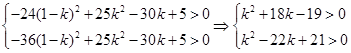
由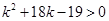 解得
解得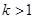 或
或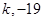 ;由
;由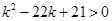 解得
解得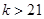 或
或 ,
,
综合得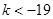 或
或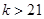 .
.
考点:等差数列的定义及求和、求通项.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com