
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性.
的单调性.
【答案】![]()
![]() ;
;![]() 当
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时, 函数
时, 函数![]() 在区间
在区间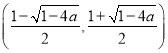 上单调递减;
上单调递减;
在区间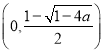 ,
,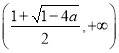 上单调递增.
上单调递增.
【解析】
![]() 根据题意,求出函数
根据题意,求出函数![]() 的导数
的导数![]() ,由导数的几何意义知函数
,由导数的几何意义知函数![]() 在
在![]() 处切线的斜率
处切线的斜率![]() ,代入点斜式方程即可求解;
,代入点斜式方程即可求解;
![]() 根据题意,求出函数
根据题意,求出函数![]() 的导数
的导数![]() ,分
,分![]() 和
和![]() 两种情况,求出
两种情况,求出![]() 所对的
所对的![]() 的取值范围,据此可以判断函数
的取值范围,据此可以判断函数![]() 的单调性.
的单调性.
![]() 当
当![]() 时,
时,![]() ,则
,则![]() ,
,
所以![]() ,由导数的几何意义可知,
,由导数的几何意义可知,
函数![]() 在
在![]() 处切线的斜率
处切线的斜率![]() ,
,
所以函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ;
;
![]() 因为函数
因为函数![]() ,
,
所以![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,因为
,因为![]() ,
,
所以![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,因为方程
时,因为方程![]() 的两根为
的两根为![]() ,
,
所以由![]() ,解得
,解得![]() 或
或![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间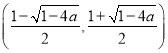 上单调递减;
上单调递减;
在区间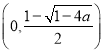 ,
,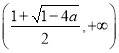 上单调递增.
上单调递增.
综上可知, 当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时, 函数
时, 函数![]() 在区间
在区间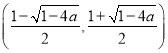 上单调递减;
上单调递减;
在区间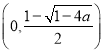 ,
,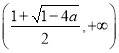 上单调递增.
上单调递增.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】2018年1月18日,国家禁毒办召开视频会议,部署开展全国禁毒示范城市创建活动,会上,贵阳成功入选为首批全国101个示范创建城市之一.为进一步推进创建工作的开展,贵阳市教育局全面部署了各中小学深入学习禁毒知识的工作.某校据此开展相关禁毒知识测试活动,如图的茎叶图是该校从甲、乙两个班级各随机抽取5名同学在一次禁毒知识测试中的成绩统计
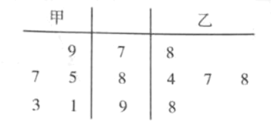
(1)请从统计学角度分析两个班级的同学在禁毒知识学习上的状况;
(2)由于测试难度较大,测试成绩达到87分以上(含87分)者即视为合格,先从茎叶图中达到合格的同学中抽取三人进行成绩分析,试求抽取到的同学中至少有两人来自甲班的概率;
(3)已知本次测试的成绩![]() 服从正态分布
服从正态分布![]() ,该校共有1000名同学参加了测试,求测试成绩在86分到97分之间的人数.
,该校共有1000名同学参加了测试,求测试成绩在86分到97分之间的人数.
(参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某美术学院2018年在山西招生,报名人数很多.工作人员在某个市区抽取了该区2018年美术招生考试成绩中200名学生的色彩和素描的初试成绩,按成绩分组,得到的频率分布表如下图所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 24 | 0.12 |
第2组 |
| ① | 0.18 |
第3组 |
| 64 | 0.32 |
第4组 |
| 60 | ② |
第5组 |
| 16 | 0.08 |
合计 | 200 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图,并由频率分布直方图估算中位数;
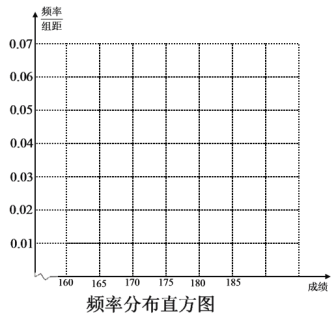
(2)为了能更清楚地了解该市学生的情况,该美院决定在复试以前先进行抽样调研.但受场地和教授人数的客观限制,决定从第3组选出3人,第4组选出2人,第5组选出1人,然后从这6人中再选出2人进行调研,求这2人均来自第三组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x﹣1|+|2x+1|<3的解集为{x|a<x<b};
(1)求a,b的值;
(2)若正实数x,y满足x+y=ab+2且不等式(yc2﹣4)x+(8cx﹣1)y≤0对任意的x,y恒成立,求实数c的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,且
,且![]() .点
.点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
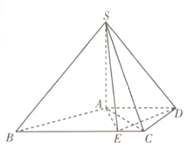
(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲市有![]() 万名高三学生参加了天一大联考,根据学生数学成绩(满分:
万名高三学生参加了天一大联考,根据学生数学成绩(满分:![]() 分)的大数据分析可知,本次数学成绩
分)的大数据分析可知,本次数学成绩![]() 服从正态分布,即
服从正态分布,即![]() ,且
,且![]() ,
,![]() .
.
(1)求![]() 的值.
的值.
(2)现从甲市参加此次联考的高三学生中,随机抽取![]() 名学生进行问卷调查,其中数学成绩高于
名学生进行问卷调查,其中数学成绩高于![]() 分的人数为
分的人数为![]() ,求
,求![]() .
.
(3)与甲市相邻的乙市也有![]() 万名高三学生参加了此次联考,且其数学成绩
万名高三学生参加了此次联考,且其数学成绩![]() 服从正态分布
服从正态分布![]() .某高校规定此次联考数学成绩高于
.某高校规定此次联考数学成绩高于![]() 分的学生可参加自主招生考试,则甲和乙哪个城市能够参加自主招生考试的学生更多?
分的学生可参加自主招生考试,则甲和乙哪个城市能够参加自主招生考试的学生更多?
附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣4x2+5x﹣4.
(1)求曲线f(x)在点(2,f(2))处的切线方程:
(2)若g(x)=f(x)+k,求g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1与圆O:x2+y2=r(r>0)交于点P(﹣1,y0).且关于直线x+y=1对称.
(1)求圆O及圆O1的方程:
(2)在第一象限内.圆O上是否存在点A,过点A作直线l与抛物线y2=4x交于点B,与x轴交于点D,且以点D为圆心的圆过点O,A,B?若存在.求出点A的坐标;若不存在.说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com