
【题目】已知A(x1 , f(x1),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(Ⅲ)当x∈[0, ![]() ]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)∵初相φ的终边经过点P(1,﹣ ![]() ), ∴φ为第四象限角,且tanφ=
), ∴φ为第四象限角,且tanφ= ![]() =﹣
=﹣ ![]() ,
,
再结合﹣ ![]() <φ<0,可得φ=﹣
<φ<0,可得φ=﹣ ![]() .
.
∵|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() =
= ![]() =
= ![]() ,
,
∴ω=3,函数f(x)=2sin(3x﹣ ![]() ).
).
(Ⅱ)令2kπ﹣ ![]() ≤3x﹣
≤3x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,
,
求得 ![]() ﹣
﹣ ![]() ≤x≤
≤x≤ ![]() +
+ ![]() ,
,
可得函数的增区间为[ ![]() ﹣
﹣ ![]() ,
, ![]() +
+ ![]() ].
].
再结合x∈[0, ![]() ],
],
可得当x∈[0, ![]() ]时函数的增区间为[0,
]时函数的增区间为[0, ![]() ].
].
(Ⅲ)∵当x∈[0, ![]() ]时,
]时,
∴3x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
f(x)∈[﹣ ![]() ,1],
,1],
故 1﹣ ![]() 的最大值为1﹣
的最大值为1﹣ ![]() =
= ![]() .
.
不等式mf(x)+2m≥f(x)恒成立,
即m≥ ![]() =1﹣
=1﹣ ![]() 恒成立,
恒成立,
∴m≥ ![]() .
.
【解析】(Ⅰ)由条件利用任意角的三角函数的定义,求得tanφ的值,可得φ的值.(Ⅱ)由条件利用正弦函数的单调性,求得函数f(x)的单调递增区间.(Ⅲ)由题意可得f(x)的值域,可得 1﹣ ![]() 的最大值,条件即m≥
的最大值,条件即m≥ ![]() =1﹣
=1﹣ ![]() 恒成立,从而求得m的范围.
恒成立,从而求得m的范围.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】“莞马”活动中的α机器人一度成为新闻热点,为检测其质量,从一生产流水线上抽取20件该产品,其中合格产品有15件,不合格的产品有5件.
(1)现从这20件产品中任意抽取2件,记不合格的产品数为X,求X的分布列及数学期望;
(2)用频率估计概率,现从流水线中任意抽取三个机器人,记ξ为合格机器人与不合格机器人的件数差的绝对值,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
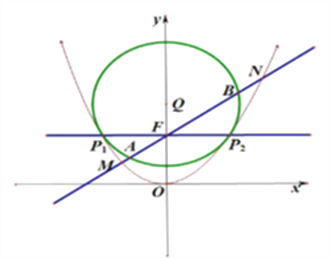
【题目】如图所示,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,
为顶点, ![]() 轴为对称轴的抛物线,且焦点在
轴为对称轴的抛物线,且焦点在![]() 轴正半轴上,圆
轴正半轴上,圆![]() .过焦点
.过焦点![]() 且与
且与![]() 轴平行的直线与抛物线交于
轴平行的直线与抛物线交于![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)直线![]() 过
过![]() 且与抛物线
且与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,且直线
,且直线![]() 的斜率
的斜率![]() ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( ) 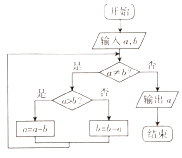
A.30
B.18
C.5
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—5:不等式选讲
设函数f(x)=|2x﹣7|+1.
(Ⅰ)求不等式f(x)≤x的解集;
(Ⅱ)若存在x使不等式f(x)﹣2|x﹣1|≤a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() ,且
,且![]() 的面积是
的面积是![]() 面积的5倍,求
面积的5倍,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是二次函数,其图象过点(0,1),且在点(-2,f(-2))处的切线方程为2x+y+3=0
(1)求f(x)的表达式;
(2)求f(x)的图象与两坐标轴所围成图形的面积;
(3)若直线x=-t(0<t<1)把f(x)的图象与两坐标轴所围成图形的面积二等分,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com