
【题目】在多面体ABCDPE中,四边形ABCD是直角梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的余弦值为
的余弦值为![]() ,
,![]() ,F为BE中点,G为PD中点.
,F为BE中点,G为PD中点.
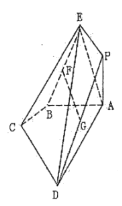
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求平面BCE与平面ADE所成角(锐角)的余弦值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,证明
,证明![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,然后证明平面
,然后证明平面![]() 平面
平面![]() ,推出
,推出![]() 平面
平面![]() ;
;
(2)在![]() 中,求出
中,求出![]() ,说明
,说明![]() ,以
,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系.求出平面
轴,建立空间直角坐标系.求出平面![]() 的一个法向量,利用空间向量的数量积求解平面
的一个法向量,利用空间向量的数量积求解平面![]() 与平面
与平面![]() 所成角的余弦值即可.
所成角的余弦值即可.
(1)取EC得中点H,连结FH,GH
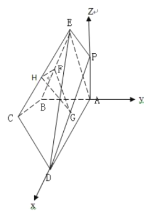
![]() 为BE中点,
为BE中点,
![]() ,
,
![]() 平面ABCD.
平面ABCD.![]() 平面ABCD,
平面ABCD,
![]() 平面ABCD
平面ABCD
![]() 为PD中点,
为PD中点,![]()
![]()
![]() 平面ABCD.
平面ABCD.![]() 平面ABCD
平面ABCD
![]() 平面ABCD
平面ABCD
![]()
![]() 平面
平面![]() 平面ABCD
平面ABCD
![]() 平面FHG
平面FHG ![]() 平面ABCD
平面ABCD
(2)在![]() 中,
中,![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() 平面
平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面
平面![]() ,
,
![]() 平面ABCD,
平面ABCD,
以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 为原点建立空间直角坐标系.
为原点建立空间直角坐标系.
![]() ,
,
设![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
设平面![]() 的一个法向量:
的一个法向量:![]() ,
,
![]() ,
,
![]()
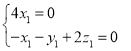 ,令
,令![]() ,
,
![]()
![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
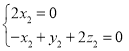 令
令![]() ,
,![]()
![]() ,
,
![]()
![]()
![]() 平面
平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值为
所成角(锐角)的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,且短轴的一个端点B与两焦点A,C组成的三角形面积为
,且短轴的一个端点B与两焦点A,C组成的三角形面积为![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:![]() 于不同的两点M,N(其中M在N的右侧),求四边形
于不同的两点M,N(其中M在N的右侧),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园有一块边长为3百米的正三角形![]() 空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道
空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道![]() 将
将![]() 分成面积之比为
分成面积之比为![]() 的两部分(点D,E分别在边
的两部分(点D,E分别在边![]() ,
,![]() 上);再取
上);再取![]() 的中点M,建造直道
的中点M,建造直道![]() (如图).设
(如图).设![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
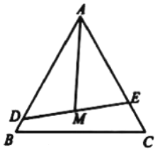
(1)分别求![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)试确定点D的位置,使两条直道的长度之和最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的长轴长为
的长轴长为![]() ,点
,点![]() 、
、![]() 、
、![]() 为椭圆上的三个点,
为椭圆上的三个点,![]() 为椭圆的右端点,
为椭圆的右端点,![]() 过中心
过中心![]() ,且
,且![]() ,
,![]() .
.

(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 是椭圆上位于直线
是椭圆上位于直线![]() 同侧的两个动点(异于
同侧的两个动点(异于![]() 、
、![]() ),且满足
),且满足![]() ,试讨论直线
,试讨论直线![]() 与直线
与直线![]() 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 与椭圆
与椭圆![]() 只有一个公共点的直线为
只有一个公共点的直线为![]() ,过点
,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求证:
,求证:![]() 与
与![]() 的交点在定直线上,并求出该定直线的方程.
的交点在定直线上,并求出该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从![]() 种服装商品,
种服装商品,![]() 种家电商品,
种家电商品,![]() 种日用商品中,选出
种日用商品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的![]() 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高![]() 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有![]() 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为![]() 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是![]() ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则![]() 最少为多少元?
最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com