
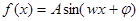 ,
,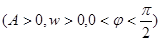 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为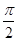 ,且图象最低点
,且图象最低点
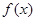 解析式
解析式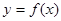 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的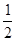 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移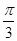 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到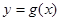 ,求
,求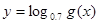 的单调递减区间
的单调递减区间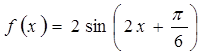 (2)
(2)
 则周期T=
则周期T= ,得到w,A的值,然后代点得到
,得到w,A的值,然后代点得到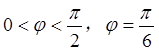 的值,得到解析式。
的值,得到解析式。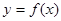 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的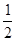 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移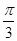 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 然后结合对数的性质得到单调区间。
然后结合对数的性质得到单调区间。 则周期T=
则周期T=
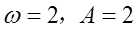 ,图象最低点M
,图象最低点M 得
得
 ,
,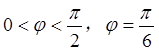
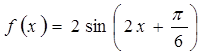 (4分)
(4分) (6 分)
(6 分) >0,
>0, 解得x 的范围是
解得x 的范围是 (8分)
(8分)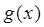 的单调递增区间,即求
的单调递增区间,即求 的单调递减区间解得x的范围是
的单调递减区间解得x的范围是 (10分)
(10分) 的单调递减区间为
的单调递减区间为


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源:不详 题型:解答题
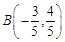 ,点C为⊙O与
,点C为⊙O与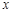 轴正半轴的交点,设∠COB=θ.
轴正半轴的交点,设∠COB=θ.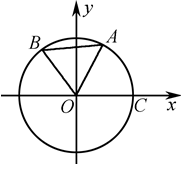
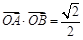 ,求点A的横坐标xA.
,求点A的横坐标xA.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
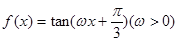 图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则
图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则 )=
)=A.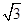 | B. | C.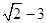 | D.-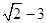 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
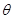 ,那么
,那么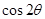 的值为 ;
的值为 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com