
已知数列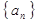 ,满足
,满足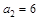 ,
,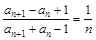
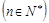 ,
,
(1)求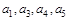 的值;
的值;
(2)猜想数列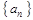 的通项公式
的通项公式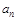 ,并用数学归纳法证明;
,并用数学归纳法证明;
(3)己知 ,设
,设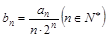 ,记
,记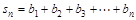 ,求
,求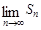 .
.
(1);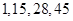 ;(2)
;(2)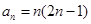 ,证明见解析;(3)3..
,证明见解析;(3)3..
解析试题分析:(1)这属于已知数列的递推关系式,求数列的项的问题,我们只要在已知递推关系式中依次令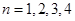 就可以依次求出
就可以依次求出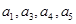 ;(2)用归纳法归纳数列的通项公式,我们可以由数列的前几项
;(2)用归纳法归纳数列的通项公式,我们可以由数列的前几项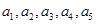 想象各项与项数
想象各项与项数 之间的联系,如
之间的联系,如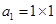 ,
,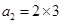 ,
,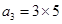 ,
,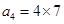 ,
,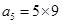 从而归纳出结论
从而归纳出结论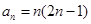 ,然后数学归纳法证明,这里数学归纳法的基础即第一步已经不需另证了,关键是第二步,假设
,然后数学归纳法证明,这里数学归纳法的基础即第一步已经不需另证了,关键是第二步,假设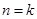 时,
时,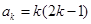 ,然后由已知条件求出
,然后由已知条件求出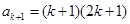 ,那么结论就是正确的;(3)按常规方法,先求
,那么结论就是正确的;(3)按常规方法,先求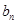 ,
,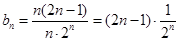 ,接着求数列
,接着求数列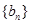 的前
的前 项和
项和 ,根据其通项公式的形式(它是一个等差数列所一个等比数列对应项相乘所得),求和用乘公比经错位相减法,求得
,根据其通项公式的形式(它是一个等差数列所一个等比数列对应项相乘所得),求和用乘公比经错位相减法,求得 ,然后借助已知极限
,然后借助已知极限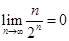 可求出极限
可求出极限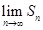 .
.
试题解析:(1) ,
,
∴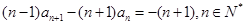 .
.
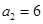 ,分别令
,分别令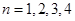 ,可得
,可得 ,
,
(2)猜想数列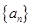 的通项公式为
的通项公式为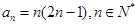 .用数学归纳法证明如下:
.用数学归纳法证明如下:
证明 (i)当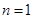 时,由(1)知结论成立;当
时,由(1)知结论成立;当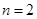 时,
时,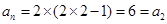 ,结论成立.
,结论成立.
(ii)假设 时,结论成立,即
时,结论成立,即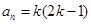 .
.
当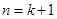 时,
时,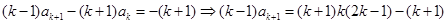
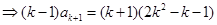
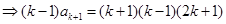 .
.
所以,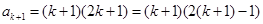 ,即
,即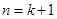 时,结论也成立.
时,结论也成立.
根据(i)和(ii)可以断定,结论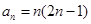 对一切正整数
对一切正整数 都成立.
都成立.
(3)由(2)知,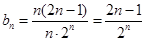 ,
, . 于是,
. 于是,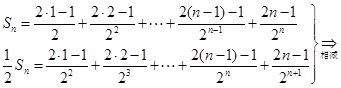
 ,
, .
.
所以,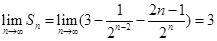 .
.
考点:(1)数列的项;(2)数学归纳法;(3)借位相减法,极限.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xk,…;y1,y2,…,yk,….
(1)分别求数列{xk}和{yk}的通项公式;
(2)令zk=xkyk,求数列{zk}的前k项和Tk,其中k∈N*,k≤2 007.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若S 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。
(1)求等比数列 的公比;
的公比;
(2)若 ,求
,求 的通项公式;
的通项公式;
(3)设 ,
, 是数列
是数列 的前
的前 项和,求使得
项和,求使得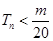 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com