
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线C交于
与曲线C交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】甲、乙两工人在同样的条件下生产,日产量相等,每天出废品的情况如下表:

则下列结论中正确的是 ( )
A. 甲生产的产品质量比乙生产的产品质量好一些
B. 乙生产的产品质量比甲生产的产品质量好一些
C. 两人生产的产品质量一样好
D. 无法判断谁生产的产品质量好一些
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
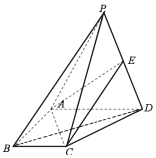
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com