
【题目】设函数f(x)= ![]() 当x∈[﹣
当x∈[﹣ ![]() ,
, ![]() ]时,恒有f(x+a)<f(x),则实数a的取值范围是( )
]时,恒有f(x+a)<f(x),则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.(﹣1, ![]() )
)
C.( ![]() ,0)
,0)
D.( ![]() ,﹣
,﹣ ![]() ]
]
 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】直线l:kx+y+4=0(k∈R)是圆C:x2+y2+4x﹣4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线m,则直线m被圆C所截得的弦长为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温x(°C)与该小卖部的这种饮料销量y(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(Ⅰ)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(Ⅱ)请根据所给五组数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(Ⅲ)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.
(参考公式: ![]() =
= 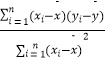 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边分别是a,b,c,则: ①若cosBcosC>sinBsinC,则△ABC一定是钝角三角形;
②若acosA=bcosB,则△ABC为等腰三角形;
③ ![]() ,
, ![]() ,若
,若 ![]() ,则△ABC为锐角三角形;
,则△ABC为锐角三角形;
④若O为△ABC的外心, ![]() ;
;
⑤若sin2A+sin2B=sin2C, ![]() ,
, 
以上叙述正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 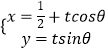 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2θ﹣2cosθ=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2θ﹣2cosθ=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() +
+ ![]() =1(a>b>0),定义椭圆的“伴随圆”方程为x2+y2=a2+b2;若抛物线x2=4y的焦点与椭圆C的一个短轴重合,且椭圆C的离心率为
=1(a>b>0),定义椭圆的“伴随圆”方程为x2+y2=a2+b2;若抛物线x2=4y的焦点与椭圆C的一个短轴重合,且椭圆C的离心率为 ![]() .
.
(1)求椭圆C的方程和“伴随圆”E的方程;
(2)过“伴随圆”E上任意一点P作椭圆C的两条切线PA,PB,A,B为切点,延长PA与“伴随圆”E交于点Q,O为坐标原点.
①证明:PA⊥PB;
②若直线OP,OQ的斜率存在,设其分别为k1 , k2 , 试判断k1k2是否为定值,若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的有__________.
①如果![]() 、
、![]() 与平面
与平面![]() 共面且
共面且![]() ,
,![]() ,那么
,那么![]() 就是平面
就是平面![]() 的一个法向量;
的一个法向量;
②设![]() :实数
:实数![]() ,
,![]() 满足
满足![]() ;
;![]() :实数
:实数![]() ,
,![]() 满足
满足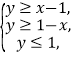 则
则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③已知椭圆![]() 与双曲线
与双曲线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的离心率,则
的离心率,则![]() ,且
,且![]() ;
;
④菱形是圆的内接四边形或是圆的外切四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE. 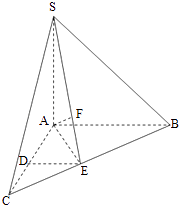
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者. 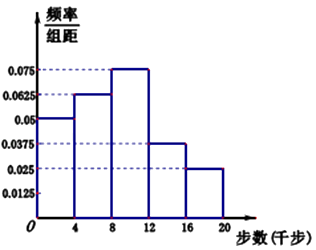
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取3人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励0元,超健康生活方式者表彰奖励20元,一般生活方式者鼓励性奖励10元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com