
【题目】已知![]() =(2asin2x,a),
=(2asin2x,a),![]() =(-1,2
=(-1,2![]() sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)=![]() +b,b>a. (1)若a>0,写出函数y=f(x)的单调递增区间;
+b,b>a. (1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[![]() ,π],值域为[2,5],求实数a与b的值.
,π],值域为[2,5],求实数a与b的值.
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]() .
.
【解析】
(1)先化简函数得f(x)= 2asin![]() +b,再求函数的单调增区间.(2)对a分类讨论,利用不等式的性质和三角函数的图像和性质,求出函数的最大值和最小值即得a和b的值.
+b,再求函数的单调增区间.(2)对a分类讨论,利用不等式的性质和三角函数的图像和性质,求出函数的最大值和最小值即得a和b的值.
(1)f(x)=-2asin2x+2![]() asinxcosx+a+b=2asin
asinxcosx+a+b=2asin![]() +b,
+b,
∵a>0,∴由2kπ-![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() 得,kπ-
得,kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z.
,k∈Z.
∴函数y=f(x)的单调递增区间是[kπ-![]() ,kπ+
,kπ+![]() ](k∈Z)。
](k∈Z)。
(2)x∈[![]() ,π]时,2x+
,π]时,2x+![]() ∈
∈![]() ,sin
,sin![]() ∈
∈![]()
当a>0时,f(x)∈[-2a+b,a+b] ∴![]() ,得
,得![]() ,
,
当a<0时,f(x)∈[a+b,-2a+b]
∴![]() ,得
,得![]() 综上知,
综上知,![]() 或
或![]() .
.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
【题目】从5本不同的科普书和4本不同的数学书中选出4本,送给4位同学,每人1本,问:
(1)如果科普书和数学书各选2本,共有多少种不同的送法?(各问用数字作答)
(2)如果科普书甲和数学书乙必须送出,共有多少种不同的送法?
(3)如果选出的4本书中至少有3本科普书,共有多少种不同的送法?
查看答案和解析>>
科目:高中数学 来源: 题型:
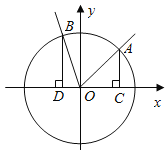
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() ,给出下列四个命题
,给出下列四个命题
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有7个不同的实根
,使得方程恰有7个不同的实根
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() .
.
(1)若直线![]() 垂直于
垂直于![]() 轴,求
轴,求![]() 的值;
的值;
(2)若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则椭圆
,则椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 关于直线
关于直线![]() 成轴对称?如果存在,求出点
成轴对称?如果存在,求出点![]() 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
(3)设直线![]() :
:![]() 上总存在点
上总存在点![]() 满足
满足![]() ,当
,当![]() 的取值最小时,求直线
的取值最小时,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足①对于任意
满足①对于任意![]() ,都有
,都有![]() ;②
;②![]() ;③
;③![]() 的图像与
的图像与![]() 轴的两个交点之间的距离为4.
轴的两个交点之间的距离为4.
(1)求![]() 的解析式;
的解析式;
(2)记![]()
①若![]() 为单调函数,求
为单调函数,求![]() 的取值范围;
的取值范围;
②记![]() 的最小值为
的最小值为![]() ,讨论函数
,讨论函数![]() 零点的个数.
零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com