(本小题满分14分)
已知数列
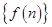
的前n项和为
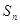
,且
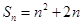
.
(Ⅰ)求数列
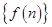
通项公式;
(Ⅱ)若
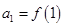
,
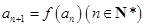
,求证数列
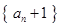
是等比数列,并求数
列
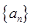
的前
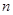
项和
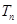
.
(Ⅰ)f(n)=2n+1(Ⅱ)证明见解析
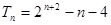
试题分析:(Ⅰ)
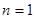
时,
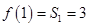
;
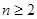
时,
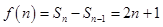
,
综上可得数列
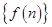
的通项为
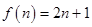
(Ⅱ)
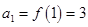
,
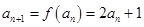
,
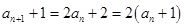
又
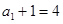
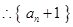
是等比数列,首项为4,公比为2,
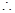
通项是
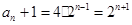
,
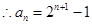
数列
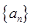
的前
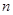
项和
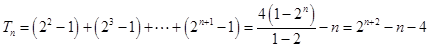
点评:由
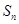
求
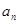
,
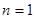
时单独考虑,分组求和是求数列前
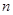
项和的常用解法
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)设数列
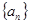
的前
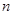
项和为
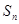
,已知
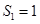
,
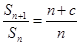
(
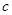
为常数,
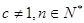
),且
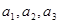
成等差数列.
(1) 求
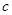
的值;
(2) 求数列
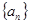
的通项公式;
(3) 若数列
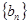
是首项为1,公比为
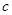
的等比数列,记
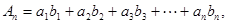
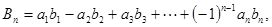
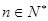
.求证:
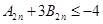
,(
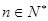
).
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
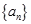
的前n项和为
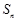
,且满足
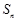
=2-

,

=1,2,3,….
(1)求数列
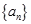
的通项公式;
(2)若数列
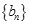
满足
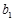
=1,且
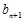
=
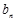
+

,求数列
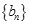
的通项公式;
(3)设
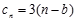
,求数列
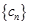
的前

项和为
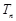
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
等差数列
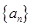
的前
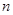
项和为
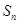
,且
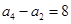
,
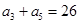
,记
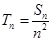
,如果存在正整数
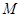
,使得对一切正整数
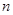
,
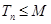
都成立,则
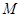
的最小值是________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知等差数列
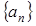
和等比数列
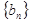
满足:
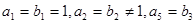
,设
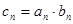
,(其中
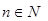
)。求数列
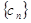
的通项公式以及前
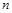
项和
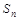
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知
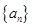
是首项为
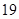
,公差为
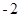
的等差数列.
(1)求通项
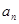
;
(2)设
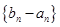
是首项为
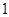
,公比为
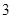
的等比数列,求数列
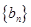
的通项公式及其前
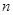
项和
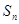
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(12分)已知数列
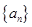
是公差不为零的等差数列,
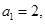
且
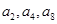
成等比数列
(1)求数列
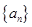
的通项公式 (2)求数列
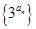
的前
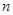
项和
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知等差数列
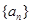
中,
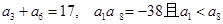
.
(Ⅰ)求
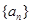
的通项公式;
(Ⅱ)调整数列
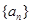
的前三项
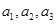
的顺序,使它成为等比数列
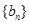
的前三项,求
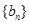
的前
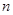
项和.
查看答案和解析>>

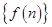 的前n项和为
的前n项和为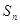 ,且
,且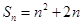 .
.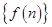 通项公式;
通项公式;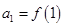 ,
,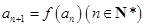 ,求证数列
,求证数列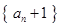 是等比数列,并求数
是等比数列,并求数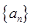 的前
的前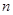 项和
项和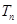 .
.  优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案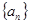 的前
的前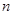 项和为
项和为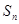 ,已知
,已知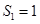 ,
,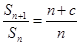 (
(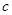 为常数,
为常数,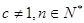 ),且
),且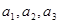 成等差数列.
成等差数列.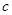 的值;
的值; 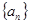 的通项公式;
的通项公式;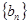 是首项为1,公比为
是首项为1,公比为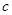 的等比数列,记
的等比数列,记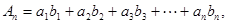
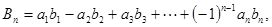
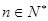
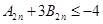 ,(
,(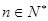 ).
).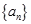 的前n项和为
的前n项和为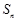 ,且满足
,且满足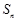 =2-
=2- ,
, =1,2,3,….
=1,2,3,….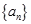 的通项公式;
的通项公式;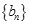 满足
满足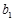 =1,且
=1,且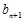 =
=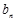 +
+ ,求数列
,求数列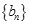 的通项公式;
的通项公式;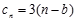 ,求数列
,求数列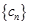 的前
的前 项和为
项和为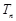 .
.