
ЁОЬтФПЁПзд2016ФъЯТАыФъЦ№СљАВЪаЧјЩЬЦЗЗПМлВЛЖЯЩЯеЧЃЌЮЊСЫЕїВщбаОПСљАВГЧЧјОгУёЖдСљАВЩЬЦЗЗПМлИёГаЪмЧщПіЃЌКЎМйЦкМфаЁУїдкСљАВЪаЧјВЛЭЌаЁЧјЗжБ№Жд50ЛЇОгУёМвЭЅНјааСЫГщВщЃЌВЂЭГМЦГіет50ЛЇМвЭЅЖдЩЬЦЗЗПЕФГаЪмМлИёЃЈЕЅЮЛЃКдЊ/ЦНЗНЃЉЃЌНЋЪеМЏЕФЪ§ОнЗжГЩ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЮхзщЃЈЕЅЮЛЃКдЊ/ЦНЗНЃЉЃЌВЂзїГіЦЕТЪЗжВМжБЗНЭМШчЭМЃК
ЮхзщЃЈЕЅЮЛЃКдЊ/ЦНЗНЃЉЃЌВЂзїГіЦЕТЪЗжВМжБЗНЭМШчЭМЃК
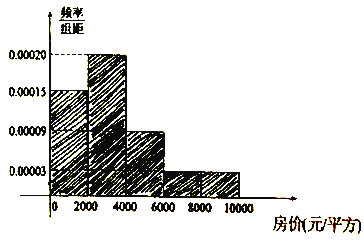
ЃЈЂёЃЉЪдИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦГіет50ЛЇМвЭЅЖдЩЬЦЗЗПЕФГаЪмМлИёЦНОљжЕЃЈЕЅЮЛЃКдЊ/ЦНЗНЃЉЃЛ
ЃЈЂђЃЉЮЊСЫзїНјвЛВНЕїВщбаОПЃЌаЁУїзМБИДгГаЪмФмСІГЌЙ§4000дЊ/ЦНЗНЕФОгУёжаЫцЛњГщГі2ЛЇНјаадйЕїВщЃЌЩшГщГіГаЪмФмСІГЌЙ§8000дЊ/ЦНЗНЕФОгУёЮЊ![]() ЛЇЃЌЧѓ
ЛЇЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3360ЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШИљОнЦЕТЪЗжВМжБЗНЭМжааЁГЄЗНаЮУцЛ§ЕШгкЖдгІЧјМфЕФИХТЪ,дйРћгУзщжажЕгыЖдгІЧјМфИХТЪГЫЛ§ЕФКЭЮЊЦНОљжЕЧѓГаЪмМлИёЦНОљжЕЃЈ2ЃЉЯШШЗЖЈЫцЛњБфСПШЁЗЈ,дйЗжБ№РћгУзщКЯЧѓЖдгІИХТЪ,СаБэПЩЕУЗжВМСа,зюКѓИљОнЪ§бЇЦкЭћЙЋЪНЧѓЦкЭћ.
ЪдЬтНтЮіЃКЃЈЂёЃЉЃЕЃАЛЇМвЭЅЖдЩЬЦЗЗПЕФГаЪмМлИёЦНОљжЕЮЊ![]() ЃЈдЊ/ЦНЗНЃЉЃЌ
ЃЈдЊ/ЦНЗНЃЉЃЌ
дђ![]()
![]() ЃЎ
ЃЎ
ЃЈЂђЃЉгЩЦЕТЪЗжВМжБЗНЭМЃЌГаЪмМлИёГЌЙ§4000дЊЕФОгУёЙВга![]() ЛЇЃЌ
ЛЇЃЌ
ГаЪмМлИёГЌЙ§8000дЊЕФОгУёЙВга![]() ЛЇЃЌ
ЛЇЃЌ
вђДЫ![]() ЕФПЩФмШЁжЕЮЊ
ЕФПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 0 | 1 | 2 |
|
|
|
|
![]()
![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕЅЕїЕндіЕФЕШБШЪ§Са![]() ТњзуЃК
ТњзуЃК ![]() ЃЌ
ЃЌ ![]()
ЃЈ1ЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ,
, ![]() ГЩСЂЕФе§ећЪ§
ГЩСЂЕФе§ећЪ§![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛЖЮдВзЖЧњЯпЃЌЧњЯпгыСНИізјБъжсЕФНЛЕуЗжБ№ЪЧ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() .
.
ЃЈЂёЃЉШєИУЧњЯпБэЪОвЛИіЭждВЃЌЩшжБЯп![]() Й§Еу
Й§Еу![]() ЧваБТЪЪЧ
ЧваБТЪЪЧ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыетИіЭждВЕФЙЋЙВЕуЕФзјБъ.
гыетИіЭждВЕФЙЋЙВЕуЕФзјБъ.
ЃЈЂђЃЉШєИУЧњЯпБэЪОвЛЖЮХзЮяЯпЃЌЧѓИУХзЮяЯпЕФЗНГЬ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжае§ШЗЕФУќЬтгаЃЈ ЃЉИі
ЃЈ1ЃЉШчЙћЦНУц![]() ЦНУц
ЦНУц![]() ЃЌФЧУДЦНУц
ЃЌФЧУДЦНУц![]() ФквЛЖЈДцдкжБЯпЦНаагкЦНУц
ФквЛЖЈДцдкжБЯпЦНаагкЦНУц![]()
ЃЈ2ЃЉШчЙћЦНУц![]() ВЛДЙжБгкЦНУц
ВЛДЙжБгкЦНУц![]() ЃЌФЧУДЦНУц
ЃЌФЧУДЦНУц![]() ФквЛЖЈВЛДцдкжБЯпДЙжБгкЦНУц
ФквЛЖЈВЛДцдкжБЯпДЙжБгкЦНУц![]()
ЃЈ3ЃЉШчЙћЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЦНУц
ЦНУц![]()
ЃЈ4ЃЉШчЙћЦНУц![]() ЦНУц
ЦНУц![]() ЃЌФЧУДЦНУц
ЃЌФЧУДЦНУц![]() ФкЫљгажБЯпЖМДЙжБгкЦНУц
ФкЫљгажБЯпЖМДЙжБгкЦНУц![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК ![]() ЃЌЙ§Еу
ЃЌЙ§Еу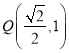 зїдВ
зїдВ![]() ЕФЧаЯпЃЌЧаЕуЗжБ№ЮЊ
ЕФЧаЯпЃЌЧаЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЧЁКУОЙ§ЭждВ
ЧЁКУОЙ§ЭждВ![]() ЕФгвЖЅЕуКЭЩЯЖЅЕуЃЎ
ЕФгвЖЅЕуКЭЩЯЖЅЕуЃЎ
ЃЈЂёЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉШчЭМЃЌЙ§ЭждВ![]() ЕФгвНЙЕу
ЕФгвНЙЕу![]() зїСНЬѕЛЅЯрДЙжБЕФЯв
зїСНЬѕЛЅЯрДЙжБЕФЯв![]() ЃЌ
ЃЌ ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ ![]() ЕФжаЕуЗжБ№ЮЊ
ЕФжаЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌжЄУїЃКжБЯп
ЃЌжЄУїЃКжБЯп![]() БиЙ§ЖЈЕуЃЌВЂЧѓДЫЖЈЕузјБъЃЎ
БиЙ§ЖЈЕуЃЌВЂЧѓДЫЖЈЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАыОЖЮЊ![]() ЕФдВаЮжНАхФкгавЛИіЯрЭЌдВаФЕФАыОЖЮЊ
ЕФдВаЮжНАхФкгавЛИіЯрЭЌдВаФЕФАыОЖЮЊ![]() ЕФаЁдВЃЌЯжНЋАыОЖЮЊ
ЕФаЁдВЃЌЯжНЋАыОЖЮЊ![]() ЕФвЛУЖгВБвХзЕНДЫжНАхЩЯЃЌЪЙећПщгВБвЭъШЋЫцЛњТфдкжНАхФкЃЌдђгВБвгыаЁдВЮоЙЋЙВЕуЕФИХТЪЮЊЃЈ ЃЉ
ЕФвЛУЖгВБвХзЕНДЫжНАхЩЯЃЌЪЙећПщгВБвЭъШЋЫцЛњТфдкжНАхФкЃЌдђгВБвгыаЁдВЮоЙЋЙВЕуЕФИХТЪЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§f(x)ЃН![]() ЃЌШєЪ§Са{an}(nЁЪN*)ТњзуЃКa1ЃН1ЃЌanЃЋ1ЃНf(an)ЃЎ
ЃЌШєЪ§Са{an}(nЁЪN*)ТњзуЃКa1ЃН1ЃЌanЃЋ1ЃНf(an)ЃЎ
(1)жЄУїЪ§Са{![]() }ЮЊЕШВюЪ§СаЃЌВЂЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЎ
}ЮЊЕШВюЪ§СаЃЌВЂЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЎ
(2)ЩшЪ§Са{cn}ТњзуЃКcnЃН![]() ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюЕФКЭSn.
ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюЕФКЭSn.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдк![]() ЩЯЕФКЏЪ§
ЩЯЕФКЏЪ§![]() ЃЌШчЙћДцдкКЏЪ§
ЃЌШчЙћДцдкКЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉЃЌЪЙЕУ
ЮЊГЃЪ§ЃЉЃЌЪЙЕУ![]() ЖдвЛЧаЪЕЪ§
ЖдвЛЧаЪЕЪ§![]() ЖМГЩСЂЃЌдђГЦ
ЖМГЩСЂЃЌдђГЦ![]() ЮЊКЏЪ§
ЮЊКЏЪ§![]() ЕФвЛИіГаЭаКЏЪ§ЃЌИјГіШчЯТУќЬтЃК
ЕФвЛИіГаЭаКЏЪ§ЃЌИјГіШчЯТУќЬтЃК
ЂйКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФвЛИіГаЭаКЏЪ§ЃЛ
ЕФвЛИіГаЭаКЏЪ§ЃЛ
ЂкКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФвЛИіГаЭаКЏЪ§ЃЛ
ЕФвЛИіГаЭаКЏЪ§ЃЛ
ЂлШєКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФвЛИіГаЭаКЏЪ§ЃЌдђ
ЕФвЛИіГаЭаКЏЪ§ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЛ
ЃЛ
ЂмжЕгђЪЧ![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ВЛДцдкГаЭаКЏЪ§.
ВЛДцдкГаЭаКЏЪ§.
Цфжае§ШЗЕФУќЬтЕФИіЪ§ЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=2sin2ЃЈ ![]() +xЃЉЉ
+xЃЉЉ ![]() cos2xЃЌ
cos2xЃЌ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФзюаЁе§жмЦкМАЕЅЕїЕнМѕЧјМфЃЛ
ЃЈ2ЃЉЕБx ![]() ЪБЃЌЧѓfЃЈxЃЉЕФзюДѓжЕКЭзюаЁжЕЃЎ
ЪБЃЌЧѓfЃЈxЃЉЕФзюДѓжЕКЭзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com