
分析 由两角和的正弦函数化简已知的等式,由平方关系列出方程,结合题意和三角函数值的符号判断出:sinθ<0、cosθ>0,联立方程后求出cosθ的值.
解答 解:由$sin(θ+\frac{π}{4})=\frac{3}{5}$得$sinθcos\frac{π}{4}+cosθsin\frac{π}{4}=\frac{3}{5}$,
则$\frac{\sqrt{2}}{2}(sinθ+cosθ)=\frac{3}{5}$,①
又sin2θ+cos2θ=1,②
因为θ是第四象限角,sinθ<0、cosθ>0,③
由①②③解得,cosθ=$\frac{{7\sqrt{2}}}{10}$,
故答案为:$\frac{{7\sqrt{2}}}{10}$.
点评 本题考查两角和的正弦函数,三角函数值的符号,以及平方关系的应用,考查方程思想,化简、计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | [1,2) | D. | [1,2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
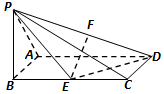 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点$({1,\frac{3}{2}})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
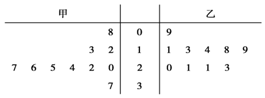 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com