
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)当![]() 时,过坐标原点
时,过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅲ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
: ![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
【答案】(Ⅰ)-2;(Ⅱ) ![]() ;(Ⅲ)参考解析
;(Ⅲ)参考解析
【解析】试题分析:(Ⅰ)先求导数,再求导数零点,最后根据导数符号变化规律,确定极小值,(Ⅱ)根据导数几何意义得切线的斜率等于切点处导数值,可得关于![]() 的方程,再利用导数研究单调性确定方程解的个数,最后根据估值得方程的解,(Ⅲ)先求切线方程得
的方程,再利用导数研究单调性确定方程解的个数,最后根据估值得方程的解,(Ⅲ)先求切线方程得![]() ,再求函数
,再求函数![]() 导数,最后根据导函数的两个零点必须相同得“转点”.
导数,最后根据导函数的两个零点必须相同得“转点”.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
所以当![]() 时,
时, ![]() 取到极小值-2.
取到极小值-2.
(Ⅱ)![]() ,所以切线的斜率
,所以切线的斜率![]() ,
,
整理得![]() ,显然
,显然![]() 是这个方程的解,
是这个方程的解,
又因为![]() 在
在![]() 上是增函数,
上是增函数,
所以方程![]() 有唯一实数解,故
有唯一实数解,故![]() .
.
(Ⅲ)当![]() 时,函数
时,函数![]() 在其图象上一点
在其图象上一点![]() 处的切线方程为
处的切线方程为 ,
,
设![]() ,则
,则![]() ,
,  ,
,
若![]() ,
, ![]() 在
在 上单调递减,所以当
上单调递减,所以当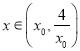 时
时![]() ,此时
,此时![]() ;
;
所以![]() 在
在![]() 上不存在“转点”.
上不存在“转点”.
若![]() 时,
时, ![]() 在
在 上单调递减,所以当
上单调递减,所以当 时
时![]() ,此时
,此时![]() ,所以
,所以![]() 在
在![]() 上不存在“转点”.
上不存在“转点”.
若![]() 时
时![]() ,即
,即![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,即点
,即点![]() 为“转点”,
为“转点”,
故函数![]() 存在“转点”,且2是“转点”的横坐标.
存在“转点”,且2是“转点”的横坐标.


科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
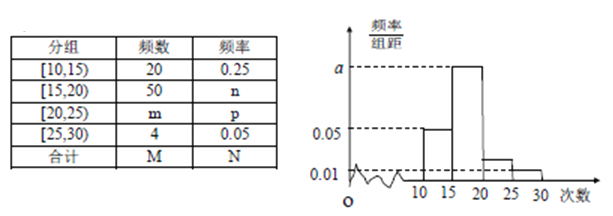
(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等的根,求实数
上有两个不等的根,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,当
,当![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在遂宁市中央商务区的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、2只白色的乒乓球(其体积,质地完全相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得统一颜色的3个球,摊主送个摸球者10元钱;若摸得非同一颜色的3个球。摸球者付给摊主2元钱。
(1)摸出的3个球中至少有1个白球的概率是多少?
(2)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com