
����Ŀ����ͼ��ij��ѧ�ס��������25��ѧ�������μ���һ�� ���ԣ���25λѧ���Ŀ��ֱ�ɵľ�Ҷͼ��������һ����������Բ���Ա��С��ɾ���ˣ���������x����ʾ������������ؼǵ�����ѧ���ɼ�����λ����ͬ��

����������������ѧ���ɼ�����λ����x��ֵ��
�������������Щ�ɼ���Ϊ�����������÷���175�� ���ϣ�����175�֣���������������ѧУ�ٴ��������������������ɼ��Ŀ�����ѡ��3������ѧУ�μӱ���������3���мװ�������һ����ѡ�ĸ��ʣ�
���𰸡���1�� x=7����2��![]()
��������
���⣨������λ����������С�������к�λ�����м��һ��������������ƽ����������������ǹŵ�����ʣ����ʱ��Ҫ�ҵ����л����¼�����![]() ������������Ҫ��Ļ����¼�������7�У����Ը���Ϊ
������������Ҫ��Ļ����¼�������7�У����Ը���Ϊ![]()
����������������װ�ѧ���ɼ�����λ��Ϊ![]() ��
��
�Ұ�ѧ���ɼ�����λ��������150+x=157����x=7�� ����4��
��������A��ʾ�¼����װ�������1����ѡ����
��װ���λ����ΪA��B���Ұ���λ����Ϊ1��2��3��
���5����ѡ��3�˵����з�������Ϊ��
��A��B��1������A��B��2������A��B��3������A��1��2������A��1��3������A��2��3����
��B��1��2������B��1��3������B��2��3������1��2��3����10������� ��8��
��������1���װ�ͬѧ���������A��1��2������A��1��3������A��2��3������B��1��2������B��1��3������B��2��3������1��2��3��7�֣� ����10��
�ɹŵ�����ʼ��㹫ʽ�ɵ�P��A��=![]() �� ����12��
�� ����12��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��n��=1+ ![]() +
+ ![]() +��+
+��+ ![]() ��n��N*���������f��2��=
��n��N*���������f��2��= ![]() ��f��4����2��f��8����
��f��4����2��f��8���� ![]() ��f��16����3��f��32����
��f��16����3��f��32���� ![]() ���ɴ����㣺��n��2ʱ���У� ��
���ɴ����㣺��n��2ʱ���У� ��
A.f��2n���� ![]() ��n��N*��
��n��N*��
B.f��2n���� ![]() ��n��N*��
��n��N*��
C.f��2n���� ![]() ��n��N*��
��n��N*��
D.f��2n���� ![]() ��n��N*��
��n��N*��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2-4ax+1+b��a��0���Ķ�����Ϊ[2��3]��ֵ��Ϊ[1��4]����g��x��=![]() ��
��
��1����a��b��ֵ��
��2��������ʽg��2x��-k2x��0��x��[1��2]�Ϻ��������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ����ְ���ij��������������ȡ50��ְ�����������ǵľ�ס���빫˾�ľ���d����λ��ǧ�ף������������ݷ���Ϊ[0��2]����2��4]����4��6]����6��8]����8��10]����10��12]�������ݻ��Ƶķֲ�Ƶ��ֱ��ͼ��ͼ��ʾ����������ְ����ס���빫˾�ľ��벻����4ǧ������Ϊ�ˣ� 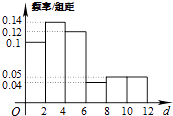
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2��2bx+a��a��b��R��
��1����a�Ӽ���{0��1��2��3}����ȡһ��Ԫ�أ�b�Ӽ���{0��1��2��3}����ȡһ��Ԫ�أ���f��x��=0ǡ�����������ʵ���ĸ��ʣ�
��2����b������[0��2]����ȡһ������a������[0��3]����ȡһ��������f��x��=0û��ʵ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������չѵ���У��˴���ֱǽ�ڵĶ���A�ع⻬�������»�����б��ľ���ϣ��˿ɿ����ʵ㣩����ľ�����б�Dz�ͬ��������������ͬ·��AB��AC��AD����ľ���ϵ�ʱ��ֱ�Ϊt1��t2��t3������֪AB��AC��AD���ļнǷֱ�Ϊ70o��90o��105o���� ��

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. ����ȷ��t1��t2��t3֮��Ĺ�ϵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ�������ǣ� ��
A.?�ա�R������f��x��=sin��2x+�գ�������ż����
B.?�����¡�R��ʹcos����+�£�=cos��+cos��
C.���� ![]() =����2��1����
=����2��1���� ![]() =����3��0������
=����3��0������ ![]() ��
�� ![]() �����ϵ�ͶӰΪ2
�����ϵ�ͶӰΪ2
D.��|x|��1���ǡ�x��1���ļȲ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��������x2��ax+a+3=0�н⡱��q���� ![]() ��a��0��[0��+�ޣ��Ϻ����������p��qΪ�����⣬p��qΪ�����⣬��ʵ��a��ȡֵ��Χ��
��a��0��[0��+�ޣ��Ϻ����������p��qΪ�����⣬p��qΪ�����⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ԲC�� ![]() +
+ ![]() =1��a��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��P��3��1������Բ�ϣ���PF1F2�����Ϊ2
=1��a��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��P��3��1������Բ�ϣ���PF1F2�����Ϊ2 ![]() ��
�� 
��1��������ԲC�ı����̣� ������F1QF2= ![]() ����QF1QF2��ֵ��
����QF1QF2��ֵ��
��2��ֱ��y=x+k����ԲC�ཻ��A��B���㣬����ABΪֱ����Բ��������ԭ�㣬��ʵ��k��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com