
设 .
.
(1)当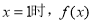 取到极值,求
取到极值,求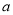 的值;
的值;
(2)当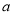 满足什么条件时,
满足什么条件时,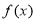 在区间
在区间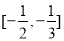 上有单调递增的区间.
上有单调递增的区间.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:选择题
函数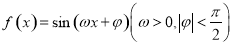 的最小正周期是
的最小正周期是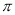 ,若其图象向右平移
,若其图象向右平移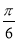 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数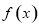 的图象( )
的图象( )
A.关于点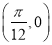 对称 B.关于直线
对称 B.关于直线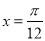 对称
对称
C.关于点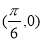 对称 D.关于直线
对称 D.关于直线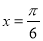 对称
对称
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
函数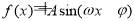 (
(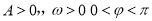 )的图象如图所示,则
)的图象如图所示,则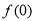 的值为 ( )
的值为 ( )

A. B.
B.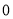 C.
C.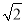 D.
D.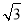
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:填空题
已知函数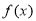 的定义域[-1,5],部分对应值如表,
的定义域[-1,5],部分对应值如表,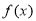 的导函数
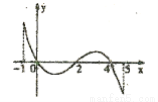
的导函数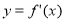 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数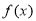 的命题;
的命题;
x | -1 | 0 | 2 | 4 | 5 |
F(x) | 1 | 2 | 1.5 | 2 | 1 |
①函数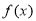 的值域为[1,2];
的值域为[1,2];
②函数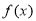 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当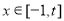 时,
时,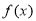 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
④当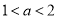 时,函数
时,函数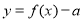 最多有4个零点.
最多有4个零点.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:填空题
函数 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有 ,则称
,则称  为单函数.例如,函数
为单函数.例如,函数 是单函数.下列命题:
是单函数.下列命题:
①函数 是单函数;②函数
是单函数;②函数 是单函数;
是单函数;
③若 为单函数,
为单函数,  且
且 ,则
,则 ;
;
④若函数 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com