
| A. | h(x)=f(x)+g(x)是偶函数 | B. | h(x)=f(x)+g(x)是奇函数 | ||
| C. | h(x)=f(x)g(x)是奇函数 | D. | h(x)=f(x)g(x)是偶函数 |
分析 利用奇偶函数的定义,即可判断.
解答 解:h(x)=f(x)+g(x)=$\frac{x}{{2}^{x}-1}$+$\frac{x}{2}$=$\frac{x}{2}•\frac{{2}^{x}+1}{{2}^{x}-1}$,h(-x)=$\frac{-x}{2}•\frac{{2}^{-x}+1}{{2}^{-x}-1}$=-$\frac{x}{2}•\frac{{2}^{x}+1}{{2}^{x}-1}$=h(x),
∴h(x)=f(x)+g(x)是偶函数;
h(x)=f(x)g(x)无奇偶性,
故选:A.
点评 本题考查函数的奇偶性,考查指数函数的性质,正确运用奇偶函数的定义是关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
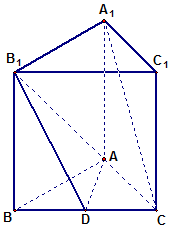 如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.
如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,BB1=8,AB=8,AC=6,BC=10,D是BC边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 父亲身高x/cm | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y/cm | 175 | 176 | 177 | 178 | 179 |
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=x+1 | C. | $\widehat{y}$=88+$\frac{1}{2}$x | D. | $\widehat{y}$=176 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com