
【题目】在三棱锥![]() 中,二面角
中,二面角![]() 、
、![]() 和
和![]() 的大小均等于
的大小均等于![]() ,
,![]() ,设三棱锥
,设三棱锥![]() 外接球的球心为
外接球的球心为![]() ,直线
,直线![]() 与平面
与平面![]() 交于点
交于点![]() .则
.则![]() ( )
( )
A.![]() B.2C.3D.4
B.2C.3D.4
【答案】D
【解析】
设![]() ,由三个二面角相等得顶点
,由三个二面角相等得顶点![]() 在底面上的射影
在底面上的射影![]() 是
是![]() 的内心,过
的内心,过![]() 外心作平面
外心作平面![]() 的垂线,外接球球心就在这条垂直线,由外接球半径求得球心到底面的距离后利用平行线性质可得结论.
的垂线,外接球球心就在这条垂直线,由外接球半径求得球心到底面的距离后利用平行线性质可得结论.
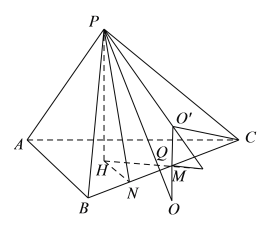
如图,作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,因此三个侧面
,因此三个侧面![]() 与底面
与底面![]() 所成的二面角相等,所以
所成的二面角相等,所以![]() 是
是![]() 的内心,
的内心,
又![]() ,设
,设![]() ,则
,则![]() ,即
,即![]() 是直角三角形,斜边是
是直角三角形,斜边是![]() ,
,
作![]() 于
于![]() ,连接
,连接![]() ,由
,由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角,所以
的平面角,所以![]() ,
,
![]() 是直角三角形,所以
是直角三角形,所以![]() ,所以
,所以![]() ,
,
设![]() 是
是![]() 中点,则
中点,则![]() 是
是![]() 的外心,连接
的外心,连接![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,连接
,连接![]() ,如图
,如图![]() 是直角梯形,
是直角梯形,
在![]() 中可得
中可得![]() ,
,
若外接球球心在![]() 位置,如图,则在直角梯形
位置,如图,则在直角梯形![]() 中,
中,![]() ,在直角
,在直角![]() 中,
中,![]() ,而
,而![]() ,
,
所以![]()
![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]() 在平面
在平面![]() 的下方(
的下方(![]() 与
与![]() 在平面
在平面![]() 的两侧),且
的两侧),且![]() .
.
直线![]() 与平面
与平面![]() 交于点
交于点![]() .则
.则![]() ,
,
由![]() 得
得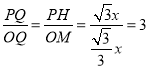 ,所以
,所以![]() .
.
故选:D.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
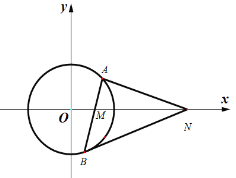
【题目】已知直线![]() :
:![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对某对象连续实施两次变换后的结果就是变换前的对象,那么我们称这种变换为“回归”变换.如:对任意一个实数,变换:取其相反数.因为相反数的相反数是它本身,所以变换“取实数的相反数”是一种“回归”变换.有下列3种变换:
①对![]() ,变换:求集合A的补集;
,变换:求集合A的补集;
②对任意![]() ,变换:求z的共轭复数;
,变换:求z的共轭复数;
③对任意![]() ,变换:
,变换:![]() (k,b均为非零实数).
(k,b均为非零实数).
其中是“回归”变换的是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
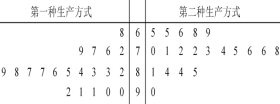
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 在底面
在底面![]() 上的射影为底面
上的射影为底面![]() 的中心点
的中心点![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() 的面积为1.
的面积为1.
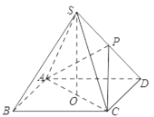
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: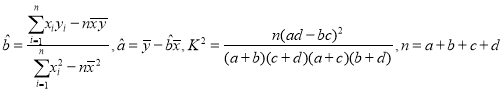 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.为了比较注射A,B两种疫苗后产生的抗体情况,选200只小鼠做实验,将这200只小鼠随机分成两组,每组100只,其中一组注射疫苗A,另一组注射疫苗B.下表1和表2分别是注射疫苗A和疫苗B后的实验结果.
表1:注射疫苗A后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射疫苗B后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成下面频率分布直方图,并比较注射两种疫苗后抗体参数的中位数大小;
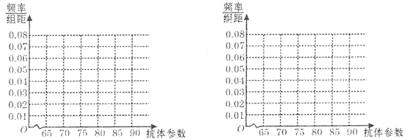
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”.
表3:
抗体参数小于75 | 抗体参数不小于75 | 合计 | |
注射疫苗A | a= | b= | |
注射疫苗B | c= | d= | |
合计 | n= |
附: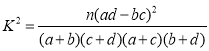
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com