
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
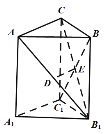
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
利用三棱柱的定义及线面垂直的性质,根据线面垂直的判定定理即可证明;
由(1)结论建立空间直角坐标系,先求出平面![]() 和平面
和平面![]() 的法向量,利用向量数量积公式即可求出二面角的余弦值.
的法向量,利用向量数量积公式即可求出二面角的余弦值.
证明:(1)因为![]() 为三棱柱,所以平面
为三棱柱,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
由题知:四边形![]() 为矩形,又因
为矩形,又因![]() 交
交![]() 于点
于点![]() ,所以
,所以![]() 为
为![]() 的中点,
的中点,
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,所以
的中位线,所以![]() .所以
.所以![]() 平面
平面![]() .
.
(2)由(1)知:![]() 两两互相垂直,所以以
两两互相垂直,所以以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示:
,如图所示:

设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() .所以
.所以![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则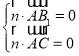 ,所以
,所以![]() ,
,
不妨令![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则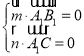 ,所以
,所以![]() ,
,
不妨令![]() ,则
,则![]() .所以
.所以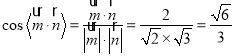 ,
,
因为平面![]() 与平面
与平面![]() 所成的角为锐角,所以二面角
所成的角为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确命题的个数为( )
①若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为4;
的方差为4;
②回归方程为![]() 时,变量x与y具有负的线性相关关系;
时,变量x与y具有负的线性相关关系;
③随机变量X服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④甲同学所在的某校高三共有5003人,先剔除3人,再按系统抽样的方法抽取容量为200的一个样本,则甲被抽到的概率为![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
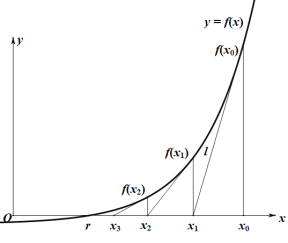
【题目】牛顿迭代法(Newtonsmethod)又称牛顿-拉夫逊方法(Newton-Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
,![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]()
![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,得到
的二次近似值.重复以上过程,得到![]() 的近似值序列.请你写出
的近似值序列.请你写出![]() 的
的![]() 次近似值与
次近似值与![]() 的
的![]() 次近似值的关系式______,若
次近似值的关系式______,若![]() ,取
,取![]() 作为
作为的初始近似值,试求
![]() 的一个根
的一个根![]() 的三次近似值______(请用分数做答).
的三次近似值______(请用分数做答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的焦点为
的焦点为![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,且点
上一点,且点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)求拋物线![]() 的标准方程;
的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,连接
两点,连接![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
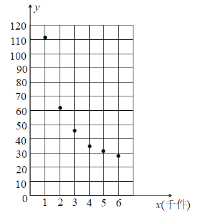
【题目】2020年初全球爆发了新冠肺炎疫情,为了防控疫情,某医疗科研团队攻坚克难研发出一种新型防疫产品,该产品的成本由原料成本及非原料成本组成,每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,根据已经生产的统计数据,绘制了如下的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用函数![]() 对两个变量的关系进行拟合.参考数据(其中
对两个变量的关系进行拟合.参考数据(其中![]() ):
):
|
|
|
|
|
|
|
0.41 | 0.1681 | 1.492 | 306 | 20858.44 | 173.8 | 50.39 |
(1)求y关于x的回归方程,并求y关于u的相关系数(精确到0.01).
(2)该产品采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为80元,则签订9千件订单的概率为0.7,签订10千件订单的概率为0.3;若单价定为70元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为30元,根据(1)的结果,要想获得更高利润,产品单价应选择80元还是70元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,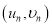 ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: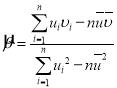 ,
,![]() ,相关系数
,相关系数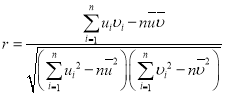 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校甲、乙、丙三名语文老师和![]() 、
、![]() 、
、![]() 三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与
三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与![]() 被派到同一所学校的概率为( )
被派到同一所学校的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是83,乙班学生成绩的平均数是86,则![]() 的值为( )
的值为( )
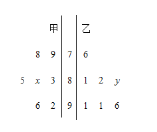
A.7B.8C.9D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图中(1)(2)(3)(4)为四个平面图形,表中给出了各平面图形中的顶点数边数以及区域数.
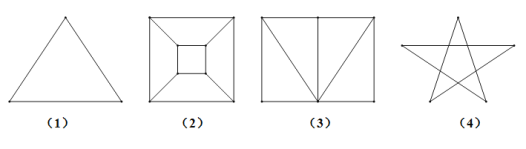
平面图形 | 顶点数 | 边数 | 区域数 |
1 | 3 | 3 | 2 |
2 | 8 | 12 | 6 |
3 | 6 | 9 | 5 |
4 | 10 | 15 | 7 |
现已知某个平面图形有1009个顶点,且围成了1006个区域,试根据以上关系确定这个平面图形的边数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com