
 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l. =
=
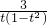
 ≤12,BM=lsinθ=
≤12,BM=lsinθ=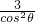 ≤6
≤6 ,cos2θ≥0
,cos2θ≥0 ,∴
,∴
 ,
, ;
; 上单调递减,在
上单调递减,在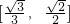 上单调递增,证明如下:
上单调递增,证明如下: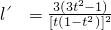 ,令l′=0可得t=
,令l′=0可得t=
 上单调递减,在
上单调递减,在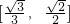 上单调递增
上单调递增 时,l取得最小值为
时,l取得最小值为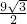 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
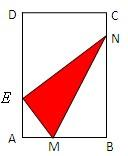 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,MN=l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,MN=l.查看答案和解析>>
科目:高中数学 来源: 题型:
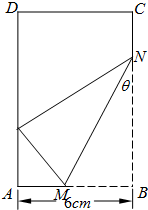 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的左边AD上,且折痕MN的两端点M、N分别位于边AB、BC上,设∠MNB=θ,则θ的取值范围为| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.
已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的端点M,N分别位于边AB,BC上,设∠MNB=θ,sinθ=t,MN长度为l.查看答案和解析>>
科目:高中数学 来源: 题型:
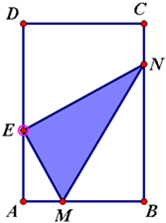 已知矩形纸片ABCD中,AB=6,AD=12,将举行制品的右下角沿线段MN折叠,使矩形的顶点B落在矩形的边AD上,记该点为E,且折痕MN的两端点M、N分别位于边AB,BC上,设∠MNB=θ,MN=l,△EMN的面积为S,
已知矩形纸片ABCD中,AB=6,AD=12,将举行制品的右下角沿线段MN折叠,使矩形的顶点B落在矩形的边AD上,记该点为E,且折痕MN的两端点M、N分别位于边AB,BC上,设∠MNB=θ,MN=l,△EMN的面积为S,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com