练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A配方和B配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
    A配方的频数分布表

    指标值分组
    		[90,94)
    		[94,98)
    		[98,102)
    		[102,106)
    		[106,110)
    频数
    		8
    		20
    		42
    		22
    		8
    B配方的频数分布表
    指标值分组
    		[90,94)
    		[94,98)
    		[98,102)
    		[102,106)
    		[106,110)
    频数
    		4
    		12
    		42
    		32
    		10
    (1)分别估计用A配方，B配方生产的产品的优质品率；
    (2)已知用B配方生产的一件产品的利润y(单位：元)与其质量指标值t的关系式为y＝从用B配方生产的产品中任取一件，其利润记为X(单位：元)，求X的分布列及数学期望．(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)

    （1）0.3，0.42（2）X的分布列为

    X
    		－2
    		2
    		4
    P
    		0.04
    		0.54
    		0.42
    E(X)＝2.68.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下：

    日最高气温t(单位：℃)
    		t≤22
    		22＜t≤28
    		28＜t≤32
    		t＞32
    天数
    		6
    		12
    		Y
    		Z
    由于工作疏忽，统计表被墨水污染，Y和Z数据不清楚，但气象部门提供的资料显示，六月份的日最高气温不高于32℃的频率为0.9.
    某水果商根据多年的销售经验，六月份的日最高气温t(单位：℃)对西瓜的销售影响如下表：
    日最高气温t(单位：℃)
    		t≤22
    		22＜t≤28
    		28＜t≤32
    		t＞32
    日销售额X(单位：千元)
    		2
    		5
    		6
    		8
    (1)求Y，Z的值；
    (2)若视频率为概率，求六月份西瓜日销售额的期望和方差；
    (3)在日最高气温不高于32℃时，求日销售额不低于5千元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校校庆，各届校友纷至沓来，某班共来了n位校友(n>8且n∈N*)，其中女校友6位，组委会对这n位校友登记制作了一份校友名单，现随机从中选出2位校友代表，若选出的2位校友是一男一女，则称为“最佳组合”．
    (1)若随机选出的2位校友代表为“最佳组合”的概率不小于，求n的最大值；
    (2)当n＝12时，设选出的2位校友代表中女校友人数为ξ，求ξ的分布列和数学期望E(ξ)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者，20名学生的名额分配为高一12人，高二6人，高三2人．
    （1）若从20名学生中选出3人做为组长，求他们中恰好有1人是高一年级学生的概率；
    （2）若将4名教师随机安排到三个年级（假设每名教师加入各年级是等可能的，且各位教师的选择是相互独立的），记安排到高一年级的教师人数为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    辽宁某大学对参加全运会的志愿者实施“社会教育实践”学分考核，因该批志愿者表现良好，该大学决定考核只有合格和优秀两个等次，若某志愿者考核为合格，授予0.5个学分；考核为优秀，授予1个学分，假设该校志愿者甲、乙、丙考核为优秀的概率分别为、、，他们考核所得的等次相互独立．
    (1)求在这次考核中，志愿者甲、乙、丙三人中至少有一名考核为优秀的概率；
    (2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量X，求随机变量X的分布列．
    (3)求X的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某班同学利用寒假进行社会实践，对年龄在的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
       
    （1）补全频率分布直方图，并求的值；
    （2）从年龄在的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知向量
    (1)若分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数，求满足的概率.
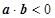    (2)若在连续区间[1,6]上取值，求满足的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    学校游园活动有这样一个游戏项目：甲箱子里装有3个白球，2个黑球，乙箱子里装有1个白球，2个黑球，这些球除颜色外完全相同．每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖(每次游戏结束后将球放回原箱)．
    (1)求在1次游戏中：
    ①摸出3个白球的概率；②获奖的概率．
    (2)求在两次游戏中获奖次数X的分布列及数学期望E(X)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两人玩猜数字游戏，规则如下：
    ①连续竞猜3次，每次相互独立；
    ②每次竞猜时，先由甲写出一个数字，记为a，再由乙猜甲写的数字，记为b，已知a，b∈{0,1,2,3,4,5}，若|a－b|≤1，则本次竞猜成功；
    ③在3次竞猜中，至少有2次竞猜成功，则两人获奖．
    求甲乙两人玩此游戏获奖的概率．

    查看答案和解析>>

    同步练习册答案