下列结论中:
(1)定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞]也是增函数,则函数f(x)在R上是增函数;
(2)若f(2)=f(-2),则函数f(x)不是奇函数;
(3)函数y=x-0.5(4)是(0,1)上的减函数;
(4)对应法则和值域相同的函数的定义域也相同;
(5)若x0是函数y=f(x)的零点,且m<x0<n,则f(m) f(n)<0一定成立;
写出上述所有正确结论的序号:________.
解:
(1)由增函数的定义中“任意性”知,两个单调区间不能并在一起,故不对;
(2)函数y=0(x∈R)既是奇函数又是偶函数,但f(2)=f(-2),故不对;
(3)考察幂函数y=x-0.5(,因-0.5<0,故(0,1)上的减函数,故正确;
(4)考察函数y=0(x∈R),但当定义域不同时,函数对应法则和值域可以相同,故不对;
(5)若x0是函数y=f(x)的零点,且m<x0<n,则f(m) f(n)不一定小于0,故不对.
故答案为:(1)(3).
分析:利用函数的奇(偶)的定义和函数相等的定义判断(2)(4)不对,根据单调函数的定义判断(1)对(3)不对.根据函数零点的定义知(5)错.
点评:本题的考点是奇(偶)函数和减函数的定义的应用,主要考查对定义中关键词“任意性”的理解.



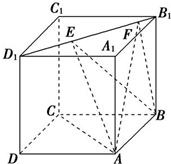 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=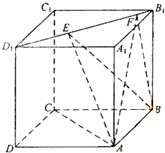 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D上有两个动点E、F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D上有两个动点E、F,且EF= 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=