
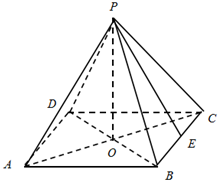
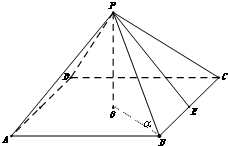
 如图,设计一个小型正四棱锥形冷水塔,其中顶点P在底面的射影为正方形ABCD的中心O,返水口E为BC的中点,冷水塔的四条钢梁(侧棱)设计长度均为10米.冷水塔的侧面选用钢板,基于安全与冷凝速度的考量,要求钢梁(侧棱)与底面的夹角α落在区间[
如图,设计一个小型正四棱锥形冷水塔,其中顶点P在底面的射影为正方形ABCD的中心O,返水口E为BC的中点,冷水塔的四条钢梁(侧棱)设计长度均为10米.冷水塔的侧面选用钢板,基于安全与冷凝速度的考量,要求钢梁(侧棱)与底面的夹角α落在区间[| π |
| 6 |
| π |
| 3 |
| 2 |
| 2 |
| 1+sin2α |
| 1-sin4α |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| 2 |
| 2 |
| OP2+OE2 |
| 2 |
| 1+sin2α |
| 1 |
| 2 |
| 1+sin2α |
| 1-sin4α |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
1-(
|
| 7 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年福建省厦门市高一(下)期末数学试卷(解析版) 题型:解答题
 内,如何设计可得侧面钢板用料最省且符合施工要求?
内,如何设计可得侧面钢板用料最省且符合施工要求?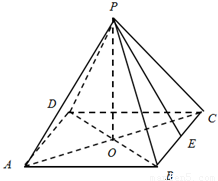
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com