
【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
(2)已知在试点前分类意识强的![]() 户居民中,有
户居民中,有![]() 户自觉垃圾分类在
户自觉垃圾分类在![]() 年以上,现在从试点前分类意识强的
年以上,现在从试点前分类意识强的![]() 户居民中,随机选出
户居民中,随机选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,求
,求![]() 分布列及数学期望.
分布列及数学期望.
参考公式: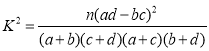 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)有![]() 的把握认为居民分类意识强与政府宣传普及工作有很大关系.见解析(2)分布列见解析,期望为1.
的把握认为居民分类意识强与政府宣传普及工作有很大关系.见解析(2)分布列见解析,期望为1.
【解析】
(1)由在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() 可得列联表,然后计算
可得列联表,然后计算![]() 后可得结论;
后可得结论;
(2)由已知![]() 的取值分别为
的取值分别为![]() ,分别计算概率得分布列,由公式计算出期望.
,分别计算概率得分布列,由公式计算出期望.
解:(1)根据在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,到分类意识强的概率为
户,到分类意识强的概率为![]() ,可得分类意识强的有
,可得分类意识强的有![]() 户,故可得
户,故可得![]() 列联表如下:
列联表如下:
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
|
|
|
试点前 |
|
|
|
合计 |
|
|
|
因为![]() 的观测值
的观测值![]() ,
,
所以有![]() 的把握认为居民分类意识强与政府宣传普及工作有很大关系.
的把握认为居民分类意识强与政府宣传普及工作有很大关系.
(2)现在从试点前分类意识强的![]() 户居民中,选出
户居民中,选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,则
,则![]() 0,1,2,3,
0,1,2,3,
故![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过原点O且斜率不为0的直线与椭圆C交于P,Q两点.
,过原点O且斜率不为0的直线与椭圆C交于P,Q两点.
(1)若![]() 为椭圆C的一个焦点,求椭圆C的标准方程;
为椭圆C的一个焦点,求椭圆C的标准方程;
(2)若经过椭圆C的右焦点的直线l与椭圆C交于A,B两点,四边形OAPB能否为平行四边形?若能,求此时直线OP的方程,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
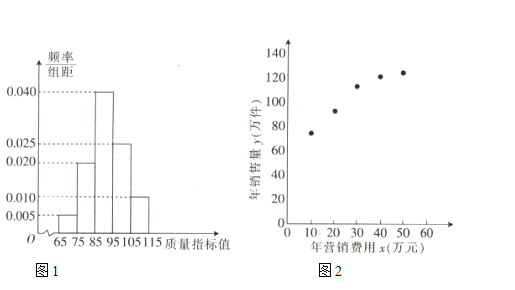
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为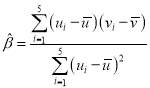 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() …是自然对数的底数),曲线
…是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的极坐标方程为
的极坐标方程为![]() (常数
(常数![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为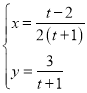 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2)若曲线![]() ,
,![]() 有两个不同的公共点,求实数
有两个不同的公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com