
【题目】△ABC的内角A、B、C的对边分别为a、b、c,已知△ABC的面积为accosB,BC的中点为D. (Ⅰ) 求cosB的值;
(Ⅱ) 若c=2,asinA=5csinC,求AD的长.
科目:高中数学 来源: 题型:
【题目】如图是求样本x1、x2、…x10平均数 ![]() 的程序框图,图中空白框中应填入的内容为( )
的程序框图,图中空白框中应填入的内容为( ) 
A.S=S+xn
B.S=S+ ![]()
C.S=S+n
D.S=S+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,ABCD是平行四边形,BDEF是矩形,ED⊥面ABCD,∠ABD= ![]() ,AB=2AD.
,AB=2AD. 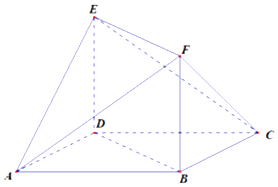
(Ⅰ)求证:平面BDEF⊥平面ADE;
(Ⅱ)若ED=BD,求AF与平面AEC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|+|x﹣3|,g(x)=a﹣|x﹣2|. (Ⅰ)若关于x的不等式f(x)<g(x)有解,求实数a的取值范围;
(Ⅱ)若关于x的不等式f(x)<g(x)的解集为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点. (Ⅰ)求P点的轨迹C的方程;
(Ⅱ)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,若kEGkFH=﹣ ![]() ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知直线l1:y=tanαx(0≤a<π,α ![]() ),抛物线C:
),抛物线C: ![]() (t为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标系 (Ⅰ)求直线l1和抛物线C的极坐标方程;
(t为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标系 (Ⅰ)求直线l1和抛物线C的极坐标方程;
(Ⅱ)若直线l1和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2 , l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设已知抛物线C:y2=2px的焦点为F1 , 过F1的直线l与曲线C相交于M,N两点.
(1)若直线l的倾斜角为60°,且|MN|= ![]() ,求p;
,求p;
(2)若p=2,椭圆 ![]() +y2=1上两个点P,Q,满足:P,Q,F1三点共线且PQ⊥MN,求四边形PMQN的面积的最小值.
+y2=1上两个点P,Q,满足:P,Q,F1三点共线且PQ⊥MN,求四边形PMQN的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域的R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足f(an+1)f( ![]() )=1(n∈N*),且a1=f(0),则下列结论成立的是( )
)=1(n∈N*),且a1=f(0),则下列结论成立的是( )
A.f(a2013)>f(a2016)
B.f(a2014)>f(a2017)
C.f(a2016)<f(a2015)
D.f(a2013)>f(a2015)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com