
【题目】已知椭圆 ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
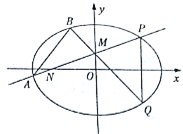
(Ⅱ)过动点![]() 的直线交
的直线交![]() 轴与点
轴与点![]() ,交
,交![]() 于点
于点![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点.过点
的中点.过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于另一点
于另一点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)设直线![]() 的斜率分别为
的斜率分别为![]() ,证明
,证明![]() 为定值;
为定值;
(ⅱ)求直线![]() 的斜率的最小值.
的斜率的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)见解析,(ⅱ)直线AB 的斜率的最小值为
;(Ⅱ)(ⅰ)见解析,(ⅱ)直线AB 的斜率的最小值为![]()
【解析】试题分析:(Ⅰ)分别计算a,b即得.
(Ⅱ)(ⅰ)设![]() ,由M(0,m),可得
,由M(0,m),可得![]() 的坐标,进而得到直线PM的斜率
的坐标,进而得到直线PM的斜率![]() ,直线QM的斜率
,直线QM的斜率![]() ,可得
,可得![]() 为定值.
为定值.
(ⅱ)设![]() .直线PA的方程为y=kx+m,直线QB的方程为y=–3kx+m.联立
.直线PA的方程为y=kx+m,直线QB的方程为y=–3kx+m.联立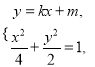 应用一元二次方程根与系数的关系得到
应用一元二次方程根与系数的关系得到![]() ,
, ![]() ,进而可得
,进而可得![]() 应用基本不等式即得.
应用基本不等式即得.
试题解析:(Ⅰ)设椭圆的半焦距为c.
由题意知![]() ,
,
所以![]() .
.
所以椭圆C的方程为![]() .
.
(Ⅱ)(ⅰ)设![]() ,
,
由M(0,m),可得![]()
所以直线PM的斜率![]() ,
,
直线QM的斜率![]() .
.
此时![]() .
.
所以![]() 为定值–3.
为定值–3.
(ⅱ)设![]() .
.
直线PA的方程为y=kx+m,
直线QB的方程为y=–3kx+m.
联立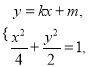
整理得![]() .
.
由![]() ,可得
,可得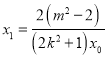 ,
,
所以![]() .
.
同理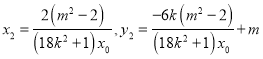 .
.
所以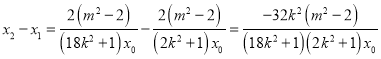 ,
,
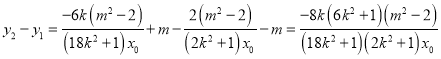 ,
,
所以![]()
由![]() ,可知k>0,
,可知k>0,
所以![]() ,等号当且仅当
,等号当且仅当![]() 时取得.
时取得.
此时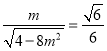 ,即
,即![]() ,符号题意.
,符号题意.
所以直线AB 的斜率的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() 的重心恰好在圆
的重心恰好在圆![]() 上,求
上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系中,已直曲线![]() ,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线
,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线 ,且直线
,且直线![]() 与C1交于A、B两点,
与C1交于A、B两点,
(1)求曲线C1的直角坐标方程,并说明它是什么曲线;
(2)设定点![]() , 求
, 求![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义为R的偶函数,且
是定义为R的偶函数,且![]() 对任意的
对任意的![]() ,都有
,都有![]() 且当
且当![]() 时,
时, ![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰好有3个不同的实数根,则
恰好有3个不同的实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图与侧视图是腰长为6的等腰直角三角形,俯视图是正方形.
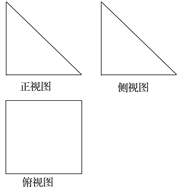
(1)请画出该几何体的直观图,并求出它的体积;
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼?试证明你的结论;
(3)在(2)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com