
分析 由已知求出$\frac{π}{3}+α$的范围,进一步求得sin($\frac{π}{3}$+α),则由sin(π+α)=-sinα=-sin[($\frac{π}{3}+α$)$-\frac{π}{3}$],展开两角差的正弦得答案.
解答 解:∵0<α<$\frac{π}{2}$,
∴$\frac{π}{3}+α$∈($\frac{π}{3},\frac{5π}{6}$),
又cos($\frac{π}{3}$+α)=$\frac{1}{3}$,
∴sin($\frac{π}{3}$+α)=$\frac{2\sqrt{2}}{3}$,
∴sin(π+α)=-sinα=-sin[($\frac{π}{3}+α$)$-\frac{π}{3}$]
=-sin($\frac{π}{3}+α$)cos$\frac{π}{3}$+cos($\frac{π}{3}+α$)sin$\frac{π}{3}$
=$-\frac{2\sqrt{2}}{3}×\frac{1}{2}$$+\frac{1}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}-2\sqrt{2}}{6}$.
故答案为:$\frac{\sqrt{3}-2\sqrt{2}}{6}$.
点评 本题考查三角函数的化简求值,关键是“拆角配角”思想的应用,是中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
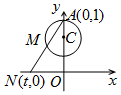 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 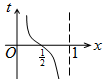 | B. | 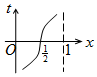 | C. | 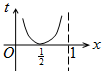 | D. | 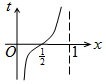 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象向左平移π个单位长度可得到y=g(x)的函象 | |
| B. | 函数y=f(x)+g(x)的值域为[-2,2] | |
| C. | 函数y=f(x)•g(x)在$[{0,\frac{π}{2}}]$上单调递增 | |
| D. | 函数y=f(x)-g(x)的图象关于点$({\frac{π}{4},0})$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com