某高店代销某工厂生产的一种商品,利润按销售额的10%提成,经市场调查:若该商品以50元一个出售,则每月销售量1万个,若售价每提高2元,则销售量在上次的基础上下降三个百分点.设以售价为52元出售为第一次提价,以后每次提价都在原来的售价上提高2元.
(1)求第n次提价的月销售额an;
(2)要使商店的月利润最大,进行几次提价最好?
解:(1)由题意知:第n次提价的单价为
50+2n,n∈N
*,
第n次提价的月销售量为1×(1-3%)
n,n∈N
*,
∴第n次提价的月销售额a
n=(50+2n)×(1-3%)
n=(50+2n)(97%)
n(万元).
(2)月利润表示为:a
n•10%,
要使得a
n•10%最大,只需a
n最大,
则
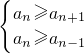
,即
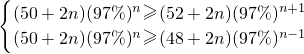
,
解得
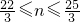
,n∈N
*,
∴当n=8,即提价8次时月利润最大.
分析:(1)由题意知:第n次提价的单价为50+2n,n∈N
*,第n次提价的月销售量为1×(1-3%)
n,n∈N
*,由此能求出第n次提价的月销售额a
n.
(2)月利润表示为:a
n•10%,要使得a
n•10%最大,只需a
n最大,则
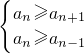
,由此能求出结果.
点评:本题考查函数在生产生活中的实际应用,解题时要认真审题,注意等价转化思想的合理运用.

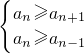 ,即
,即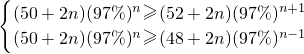 ,
,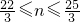 ,n∈N*,
,n∈N*,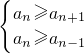 ,由此能求出结果.
,由此能求出结果.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案