
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: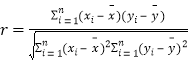 ,回归直线方程是
,回归直线方程是![]() ,
,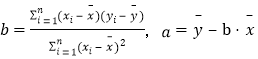 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知4名学生和2名教师站在一排照相,求:
(1)中间二个位置排教师,有多少种排法?
(2)首尾不排教师,有多少种排法?
(3)两名教师不站在两端,且必须相邻,有多少种排法?
(4)两名教师不能相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ②④D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若x4(x+4)8=a0+a1(x+3)+a2(x+3)2+…+a12(x+3)12,则log2(a1+a3+…+a11)=( ).
A. 4B. 8C. 12D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com