
【题目】如图,等腰梯形![]() 中,
中,![]()
![]() ,
,![]() ,E为CD中点,将
,E为CD中点,将![]() 沿AE折到
沿AE折到![]() 的位置.
的位置.
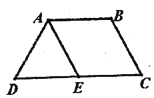
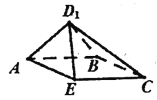
(1)证明:![]() ;
;
(2)当折叠过程中所得四棱锥![]() 体积取最大值时,求直线
体积取最大值时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)证明:直线![]() 上的点都在
上的点都在![]() 的外部.
的外部.
(2)若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 的内部或
的内部或![]() 上,求
上,求![]() 的最小值.
的最小值.
(3)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中三年级有AB两个班,各有50名同学,这两个班参加能力测试,成绩统计结果如表:
AB班成绩的频数分布表
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
A班频数 | 4 | 8 | 23 | 9 | 6 |
B班频数 | 7 | 12 | 13 | 10 | 8 |
(1)试估计AB两个班的平均分;
(2)统计学中常用M值作为衡量总体水平的一种指标,已知M与分数t的关系式为:M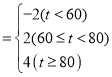 .
.
分别求这两个班学生成绩的M总值,并据此对这两个班的总体水平作简单评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,且对一切
,且对一切![]() ,均有
,均有![]() .
.
(1)求证:数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)设![]() (
(![]() ),记数列
),记数列![]() 的前n项和为
的前n项和为![]() ,问:是否存在正整数
,问:是否存在正整数![]() ,对一切
,对一切![]() ,均有
,均有![]() 恒成立.若存在,求出所有正整数
恒成立.若存在,求出所有正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的中心为
的中心为![]() ,一个方向向量为
,一个方向向量为![]() 的直线
的直线![]() 与
与![]() 只有一个公共点
只有一个公共点![]()
(1)若![]() 且点
且点![]() 在第二象限,求点
在第二象限,求点![]() 的坐标;
的坐标;
(2)若经过![]() 的直线
的直线![]() 与
与![]() 垂直,求证:点
垂直,求证:点![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
(3)若点![]() 、
、![]() 在椭圆上,记直线
在椭圆上,记直线![]() 的斜率为
的斜率为![]() ,且
,且![]() 为直线
为直线![]() 的一个法向量,且
的一个法向量,且![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图圆锥PO,轴截面PAB是边长为2的等边三角形,过底面圆心O作平行于母线PA的平面,与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到其顶点E的距离为( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点E,F分别是棱长为2的正方体![]() 的棱AB,
的棱AB,![]() 的中点.如图,以C为坐标原点,射线CDCB
的中点.如图,以C为坐标原点,射线CDCB![]() 分别是x轴y轴z轴的正半轴,建立空间直角坐标系.
分别是x轴y轴z轴的正半轴,建立空间直角坐标系.
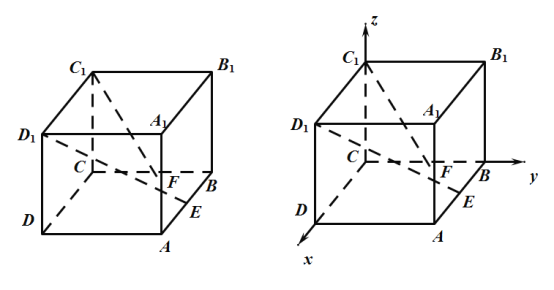
(1)求向量![]() 与
与![]() 的数量积;
的数量积;
(2)若点M,N分别是线段![]() 与线段
与线段![]() 上的点,问是否存在直线MN,
上的点,问是否存在直线MN,![]() 平面ABCD?若存在,求点M,N的坐标;若不存在,请说明理由.
平面ABCD?若存在,求点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为
底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为![]() . 求:
. 求:
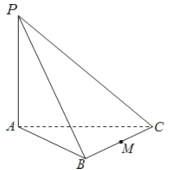
(1)三棱锥![]() 的体积;
的体积;
(2)异面直线PM与AC所成角的大小. (结果用反三角函数值表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
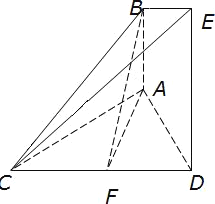
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求直线BF和平面BCE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com