
【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
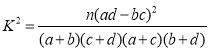
【答案】(1)列联表如图
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | 10 | 1000 |
甲不在现场 | 490 | 10 | 500 |
总数/件 | 1480 | 20 | 1500 |
在某种程度上可以认为甲在不在现场与产品质量有关。
(2)能在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”。
【解析】
(1)先由数据得出列联表,通过计算![]() 的值得出答案。
的值得出答案。
(2)由表中数据可得![]() 的观测值,进而得出答案。
的观测值,进而得出答案。
(1)根据题中所给数据得出列联表如图
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | 10 | 1000 |
甲不在现场 | 490 | 10 | 500 |
总数/件 | 1480 | 20 | 1500 |
由列联表看出![]()
因为![]() 相差较大,所以在某种程度上可以认为甲在不在现场与产品质量有关。
相差较大,所以在某种程度上可以认为甲在不在现场与产品质量有关。
(2)由表中数据可得![]() 的观测值
的观测值![]()
所以能在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)试问:函数![]() 的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
(3)若方程![]() 的三个实数根
的三个实数根![]() 、
、![]() 、
、![]() 满足:
满足:![]() <
<![]() <
<![]() ,且
,且![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,
,![]() 为平面上的动点,过点
为平面上的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为直线
为直线![]() 上一点,且满足
上一点,且满足![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为
的长度为![]() ,在线段
,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:

记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与椭圆
与椭圆![]() 的离心率相同.
的离心率相同.

(1)求![]() 的值;
的值;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,交椭圆
,交椭圆![]() 于另一点
于另一点![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 之间).①求
之间).①求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点);②设
为坐标原点);②设![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试探究点
,试探究点![]() 是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com