
【题目】已知函数 ![]() ,
, ![]() .
. ![]() 在
在 ![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求实数 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上恒成立,求实数
上恒成立,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 的对称轴为
的对称轴为 ![]() ,又
,又 ![]() ,所以
,所以 ![]() 在
在 ![]() 上单调递增,
上单调递增,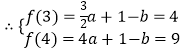 ,解得
,解得 ![]()
(2)解: ![]() ,
, ![]() ,令
,令 ![]() ,则
,则 ![]() ,
,
不等式 ![]() 可化为
可化为 ![]() ,所以,问题等价于
,所以,问题等价于 ![]() 在
在 ![]() 上恒成立,
上恒成立,
因为 ![]() ,则:
,则: ![]() ,所以:
,所以: ![]()
(3)解:令 ![]() ,图像如下:
,图像如下: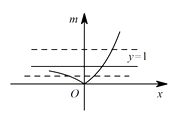
则方程 ![]() 有三个不同的实数根,等价于关于
有三个不同的实数根,等价于关于 ![]() 的方程
的方程 ![]() 有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.将
有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.将 ![]() 整理成:
整理成: ![]() ,
,
若一根等于1,一根大于0且小于1,将 ![]() 代入得
代入得 ![]() ,此时,
,此时, ![]() 只有唯一的根,不符要求,
只有唯一的根,不符要求,
所以,情况为:一根大于1,一根大于0且小于1,
令 ![]() ,则需满足
,则需满足 ![]() ,解得
,解得 ![]() .综上所述:
.综上所述: ![]() 为所求
为所求
【解析】(1)由一元二次函数的性质可得该二次函数的对称轴为x=1,故可得 f ( x ) 在 x ∈ [ 3 , 4 ] 上单调递增,结合二次函数图像的特点限制边界点的函数值进而得到关于a、b的方程组,解出其值即可。(2)由(1)的结果得到f(x) 的解析式,再由题意得到F(x)的解析式。利用整体思想设t=log2 x,根据已知的x的取值范围得出t的取值范围,由此已知的不等式即可转化为 k ≤ ![]()
![]() + 1 在 t ∈ [
+ 1 在 t ∈ [ ![]() , 2 ] 上恒成立的问题,借助二次函数在指定区间上的最值情况即可得出结果。(3)利用数形结合法结合已知条件得出方程有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,利用二次函数根的情况限制边界点的函数值,进而得到关于λ 的不等式组解出其取值范围即可。
, 2 ] 上恒成立的问题,借助二次函数在指定区间上的最值情况即可得出结果。(3)利用数形结合法结合已知条件得出方程有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,利用二次函数根的情况限制边界点的函数值,进而得到关于λ 的不等式组解出其取值范围即可。


科目:高中数学 来源: 题型:
【题目】如图,F1、F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为( ) 
A.![]()
B.2
C.![]() ﹣1
﹣1
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
[40,50) | 5 | 2 |
[50,60) | 10 | 4 |
[60,70) | 15 | 12 |
[70,80) | 10 | 6 |
[80,90) | 5 | 4 |
[90,100) | 5 | 5 |
(Ⅰ)若从分数在[70,80),[80,90)的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax+ ![]() ﹣1. (Ⅰ)当a=1时,求曲线f(x)在x=1处的切线方程;
﹣1. (Ⅰ)当a=1时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数g(x)=x2﹣2bx﹣ ![]() ,若对于x1∈[1,2],x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
,若对于x1∈[1,2],x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() . (Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
. (Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设函数 ![]() ,若在[1,e]上至少存在一点x0 , 使得f(x0)≥g(x0)成立,求实数a的取值范围.
,若在[1,e]上至少存在一点x0 , 使得f(x0)≥g(x0)成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com