
【题目】下列命题正确的是( )
A.已知实数a,b,则“a>b”是“a2>b2”的必要不充分条件
B.“存在x0∈R,使得 ![]() ”的否定是“对任意x∈R,均有x2﹣1>0”
”的否定是“对任意x∈R,均有x2﹣1>0”
C.函数 ![]() 的零点在区间
的零点在区间 ![]() 内
内
D.设m,n是两条直线,α,β是空间中两个平面,若m?α,n?β,m⊥n,则α⊥β
【答案】C
【解析】解:已知实数a,b,由a>b,不一定有a2>b2 , 反之由a2>b2 , 不一定有a>b,则“a>b”是“a2>b2”的既不充分也不必要条件,故A错误;
“存在x0∈R,使得 ![]() ”的否定是“对任意x∈R,均有x2﹣1≥0”,故B错误;
”的否定是“对任意x∈R,均有x2﹣1≥0”,故B错误;
∵函数 ![]() 与y=
与y= ![]() 均为实数集上的增函数,∴函数
均为实数集上的增函数,∴函数 ![]() 为实数集上的真数,
为实数集上的真数,
又 ![]() ,
, ![]() ,∴函数
,∴函数 ![]() 的零点在区间
的零点在区间 ![]() 内,故C正确;
内,故C正确;
设m,n是两条直线,α,β是空间中两个平面,若mα,nβ,m⊥n,则α与β相交或α∥β,故D错误.
故选:C.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() ;
;
(II)当直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() 时,求证:
时,求证: ![]() ;
;
(III)在(II)的条件下,求异面直线![]() 与
与![]() 所成的余弦值.
所成的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正三棱锥P﹣ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B﹣PA﹣C大小的取值范围是( ![]() ,π);
,π);
②若MN⊥AM,则PC与平面PAB所成角的大小为 ![]() ;
;
③过点M与异面直线PA和BC都成 ![]() 的直线有3条;
的直线有3条;
④若二面角B﹣PA﹣C大小为 ![]() ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成 ![]() 的直线有3条.
的直线有3条.
正确的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .建立如图所示的空间直角坐标系.
.建立如图所示的空间直角坐标系.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于 ![]() ;
;
(2)椭圆经过点(﹣6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中: ①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )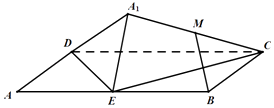
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com