
【题目】如图,在透明塑料制成的长方体ABCD﹣A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: ①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )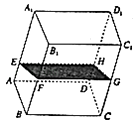
A.②③④
B.①②④
C.①③④
D.①②③
【答案】C
【解析】解:①水的部分始终呈棱柱状;从棱柱的特征平面AA1B1B平行平面CC1D1D即可判断①正确;②水面四边形EFGH的面积不改变;EF是可以变化的EH不变的,所以面积是改变的,②是不正确的③棱A1D1始终与水面EFGH平行;由直线与平面平行的判断定理,可知A1D1∥EH,所以结论正确;④当E∈AA1时,AE+BF是定值.水的体积是定值,高不变,所以底面面积不变,所以正确.
故选:C.
①水的部分始终呈棱柱状;从棱柱的特征平面判断即可;②水面四边形EFGH的面积不改变;可以通过EF 的变化EH不变判断正误;③棱A1D1始终与水面EFGH平行;利用直线与平面平行的判断定理,推出结论;④当E∈AA1时,AE+BF是定值.通过水的体积判断即可.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)= ![]() ,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
A.(0,1)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2 ![]() ,(其中,t为关税的税率,且t∈[0,
,(其中,t为关税的税率,且t∈[0, ![]() ),x为市场价格,b,k为正常数),当t=
),x为市场价格,b,k为正常数),当t= ![]() 时的市场供应量曲线如图.
时的市场供应量曲线如图. 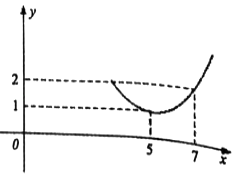
(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2 ![]() ,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足g(3)=8,又定义域为实数集R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)讨论函数y=f(x)的单调性;
(2)若对任意的t∈R,不等式f(2t﹣3t2)+f(t2﹣k)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2﹣2x(a<0)
ax2﹣2x(a<0)
(1)若函数f(x)在定义域内单调递增,求a的取值范围;
(2)若a=﹣ ![]() 且关于x的方程f(x)=﹣
且关于x的方程f(x)=﹣ ![]() x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com