
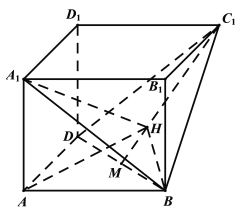
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() ,
,![]() ,
,![]() 均为正方形,点M是
均为正方形,点M是![]() 的中点,点H在线段
的中点,点H在线段![]() 上,且
上,且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为
的焦距为![]() ,且C过点
,且C过点![]() .
.
(1)求椭圆C的方程;
(2)设![]() 、
、![]() 分别是椭圆C的下顶点和上顶点,P是椭圆上异于
分别是椭圆C的下顶点和上顶点,P是椭圆上异于![]() 、
、![]() 的任意一点,过点P作
的任意一点,过点P作![]() 轴于M,N为线段PM的中点,直线
轴于M,N为线段PM的中点,直线![]() 与直线
与直线![]() 交于点D,E为线段
交于点D,E为线段![]() 的中点,O为坐标原点,则
的中点,O为坐标原点,则![]() 是否为定值,若是,请求出定值;若不是,请说明理由.
是否为定值,若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左,右焦点分别为
,其左,右焦点分别为![]() ,
,![]() ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且![]() ,
,![]() ,其中O为坐标原点.
,其中O为坐标原点.
(1)求椭圆C的方程;
(2)过点![]() ,且斜率为
,且斜率为![]() 的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在
的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在![]() 轴上截距的最大值.
轴上截距的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如147表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 37 | 104 | 147 | 196 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位.为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区.由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:①截至2018年己登记在册的私家车业主拥有竞拍资格;②每车至多中请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;③根据物价部门的规定,竞价不得超过1200元;④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主,进行了竞拍意向的调查,并对他们的拟报竞价进行了统计,得到如图频率分布直方图:

(i)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ii)如果所有符合条件的车主均参与竞拍,利用样本估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式及数据:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: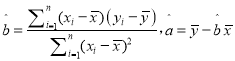 ;
;.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛决赛的500名同学编号为:001,002,...,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽到的号码为005,这500名学生分别在三个考点考试,从001到200在第一考点,从201到365在第二考点,从366到500在第三考点,则第二考点被抽中的人数为( )
A. 15B. 16C. 17D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4第一小组的频数是5.
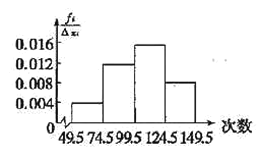
(1)求第四小组的频率和该组参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位效落在第几小组内?
(3)从第一小组中选出2人,第三小组中选出3人组成队伍代表学校参加区里的小学生体质测试,在测试的某一环节,需要从这5人中任选两人参加测试,求这两人来自同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
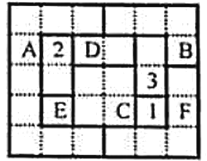
【题目】四色猜想是世界三大数学猜想之一,1976年美国数学家阿佩尔与哈肯证明了四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为1,粗实线围成的各区域(如区域D由两个边长为1的小正方形构成)上分别标有数字1,2,3,4的四色地图符合四色定理,区域A、B、C、D、E、F标记的数字丢失若在该四色地图上随机取一点,则恰好取在标记为4的区域的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com