
【题目】如图,ABCD与ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:
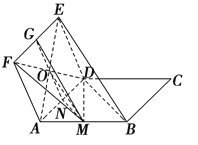
(1)BE∥平面DMF;
(2)平面BDE∥平面MNG.
【答案】见解析
【解析】
试题分析:(1)欲证线面平行常转化为找线与面中的一条直线平行.
本题中可结合题中的中点条件,找线BE与面中的线MO平行得证.
(2)证面面平行,需运用面与面平行的判定找线与面平行,
利用中点条件找出两条相交直线DE和BD与面BDE平行得证.
试题解析:(1)如图,连接AE,则AE必过DF与GN的交点O,连接MO,
则MO为△ABE的中位线,所以BE∥MO,
又BE平面DMF,MO平面DMF,所以BE∥平面DMF.
(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN,
又DE平面MNG,GN平面MNG,所以DE∥平面MNG.
又M为AB中点,所以MN为△ABD的中位线,所以BD∥MN,
又BD平面MNG,MN平面MNG,所以BD∥平面MNG,又DE与BD为平面BDE 内的两条相交直线, 所以平面BDE∥平面MNG.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系内从点P1(0,0)作x轴的垂线交曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2.再从P2作x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2;…;Pn,Qn,记![]() 点的坐标为(
点的坐标为(![]() ,0)(k=1,2,…,n).
,0)(k=1,2,…,n).

(1)试求![]() 与
与![]() 的关系(k=2,…,n);
的关系(k=2,…,n);
(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线![]() ,已知过点
,已知过点![]() 的直线的参数方程为:
的直线的参数方程为: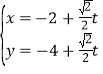 (t为参数),直线与曲线C分别交于M,N.
(t为参数),直线与曲线C分别交于M,N.
(Ⅰ)写出曲线C和直线的普通方程;
(Ⅱ)若![]() 成等比数列,求a的值.
成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( ) 
A.35
B.20
C.18
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(
=1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P( ![]() ,
, ![]() )在椭圆E上.
)在椭圆E上.
(1)求椭圆E的方程;
(2)设不过原点O且斜率为 ![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,
证明:︳MA︳︳MB︳=︳MC︳︳MD︳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的正四棱锥P-ABCD中,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论:
①PC∥平面OMN;
②平面PCD∥平面OMN;
③OM⊥PA;
④直线PD与直线MN所成角的大小为90°.
其中正确结论的序号是______.(写出所有正确结论的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com