
【题目】湖北省从2021年开始将全面推行新高考制度,新高考“3+1+2”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为A,B,C,D,E五个等级,确定各等级人数所占比例分别为15%,35%,35%,13%,2%,等级考试科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 | A | B | C | D | E |
比例 | 15% | 35% | 35% | 13% | 2% |
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]() ,其中
,其中![]() 、
、![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,Y表示原始分,T表示转换分,当原始分为
分别表示等级分区间的最低分和最高分,Y表示原始分,T表示转换分,当原始分为![]() 、
、![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]() ,假设小明同学的生物考试成绩信息如下表:
,假设小明同学的生物考试成绩信息如下表:
考试科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
生物 | 75分 | B等级 |
|
|
设小明转换后的等级成绩为T,根据公式得:![]() ,所以
,所以![]() (四舍五入取整),小明最终生物等级成绩为77分.已知某学校学生有60人选了政治,以期中考试成绩为原始成绩转换该学校选政治的学生的政治等级成绩,其中政治成绩获得A等级的学生原始成绩统计如下表:
(四舍五入取整),小明最终生物等级成绩为77分.已知某学校学生有60人选了政治,以期中考试成绩为原始成绩转换该学校选政治的学生的政治等级成绩,其中政治成绩获得A等级的学生原始成绩统计如下表:
成绩 | 90 | 86 | 81 | 80 | 79 | 78 | 75 |
人数 | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
(1)从政治成绩获得A等级的学生中任取3名,求至少有2名同学的等级成绩不小于93分的概率;
(2)从政治成绩获得A等级的学生中任取4名,设4名学生中等级成绩不小于93分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
【答案】(1)![]() (2)见详解
(2)见详解
【解析】
(1)根据已知可得,![]() 等级的学生原始分区间的最低和最高分为
等级的学生原始分区间的最低和最高分为![]() 和
和![]() ,等级分区间的最低和最高分为
,等级分区间的最低和最高分为![]() 和
和![]() ,设政治成绩获得
,设政治成绩获得![]() 等级的学生原始成绩为
等级的学生原始成绩为![]() ,等级成绩为
,等级成绩为![]() ,利用转换公式可得
,利用转换公式可得![]() ,由等级成绩不小于
,由等级成绩不小于![]() ,可求出原始成绩,对照原始成绩表,再计算概率即得;(2)由(1)知等级成绩不小于
,可求出原始成绩,对照原始成绩表,再计算概率即得;(2)由(1)知等级成绩不小于![]() 分人数为
分人数为![]() 人,获得
人,获得![]() 等级的学生有
等级的学生有![]() 人,可得
人,可得![]() 的可能取值为
的可能取值为![]() ,计算出对应的概率,可得分布列,再由期望的计算公式,即得.
,计算出对应的概率,可得分布列,再由期望的计算公式,即得.
(1)设政治成绩获得![]() 等级的学生原始成绩为
等级的学生原始成绩为![]() ,等级成绩为
,等级成绩为![]() ,由转换公式得
,由转换公式得![]() ,即
,即![]() ,则
,则![]() ,解得
,解得![]() .
.
根据成绩统计表显示满足![]() 的同学只有
的同学只有![]() 人,获得
人,获得![]() 等级的学生有
等级的学生有![]() 人,故从政治成绩获得
人,故从政治成绩获得![]() 等级的学生中任取
等级的学生中任取![]() 名,至少有
名,至少有![]() 名同学的成绩不小于
名同学的成绩不小于![]() 分的概率为
分的概率为![]() .
.
(2)由题意,等级成绩不小于![]() 分人数为
分人数为![]() 人,获得
人,获得![]() 等级的学生有
等级的学生有![]() 人,
人,![]() 的可能取值为
的可能取值为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
则![]() 的期望为:
的期望为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
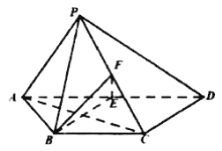
【题目】如图,在四棱锥P—ABCD中,AP⊥CD,AD∥BC,AB=BC=1,AD=2,E,F分别为AD,PC的中点.求证:
(1)AP∥平面BEF;
(2)平面BEF⊥平面PAC.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| …… |
获得奖券的金额(元) | 28 | 58 | 88 | 128 | …… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为400元的商品,则消费金额为320元,然后还能获得对应的奖券金额为28元.于是,该顾客获得的优惠额为:![]() 元.设购买商品得到的优惠率
元.设购买商品得到的优惠率![]() .试问:
.试问:
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)当商品的标价为![]() 元时,试写出顾客得到的优惠率y关于标价x元之间的函数关系式;
元时,试写出顾客得到的优惠率y关于标价x元之间的函数关系式;
(3)当顾客购买标价不超过600元的商品时,该顾客是否可以得到超过30%的优惠率?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,AP⊥CD,AD∥BC,AB=BC=1,AD=2,E,F分别为AD,PC的中点.求证:
(1)AP∥平面BEF;
(2)平面BEF⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲乙两地某月12时的气温状况,选取该月5天中12时的气温数据(单位:![]() )制成如图所示的茎叶图,考虑以下结论:
)制成如图所示的茎叶图,考虑以下结论:

①甲地该月12时的平均气温低于乙地该月12时的平均气温;
②甲地该月12时的平均气温高于乙地该月12时的平均气温;
③甲地该月12时的气温的标准差小于乙地该月12时的气温的标准差;
④甲地该月12时的气温的标准差大于乙地该月12时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值为-1,且关于
的最小值为-1,且关于![]() 的方程
的方程![]() 的两根为0和-2.
的两根为0和-2.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() 其中
其中![]() ,求函数
,求函数![]() 在
在![]() 时的最大值
时的最大值![]() ;
;
(3)若![]() (
(![]() 为实数),对任意
为实数),对任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com