
 <?<
<?< ),给出下列4个论断:(1)图象关于x=
),给出下列4个论断:(1)图象关于x= 对称(2)图象关于点(
对称(2)图象关于点( ,0)对称 (3)最小正周期是π (4)在[-
,0)对称 (3)最小正周期是π (4)在[- ,0]上是增函数以其中两个论断作为条件,余下论断为结论,写出你认为正确的两个命题:(1)________.(2)________.
,0]上是增函数以其中两个论断作为条件,余下论断为结论,写出你认为正确的两个命题:(1)________.(2)________. +∅=kπ+
+∅=kπ+ ,k∈z. 由②得ω
,k∈z. 由②得ω  +∅=kπ,k∈z.
+∅=kπ,k∈z.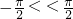 ,故有ω=2,∅=
,故有ω=2,∅= .
. ,其周期为π.
,其周期为π.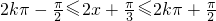 ,可得
,可得 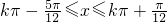 .
.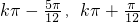 ],k∈z.
],k∈z.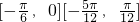 ,
,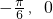 ]上是增函数,
]上是增函数, +∅=kπ+
+∅=kπ+ ,k∈z.再由
,k∈z.再由 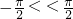 可得φ=
可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ).
). ,0)对称,由(1)可得 f(x)在区间[
,0)对称,由(1)可得 f(x)在区间[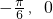 ]上是增函数.
]上是增函数. +∅=kπ+
+∅=kπ+ ; 再由②得ω
; 再由②得ω  +∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④.
+∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④. +∅=kπ+
+∅=kπ+ ,k∈z,结合∅的范围可得φ=
,k∈z,结合∅的范围可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ),由此推出②④成立.
),由此推出②④成立.

科目:高中数学 来源: 题型:
| π |
| 6 |
| 3 |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
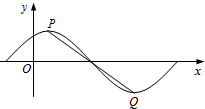 已知函数f(x)=sin(ωx+
已知函数f(x)=sin(ωx+| π |
| 3 |
| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com