
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增. (Ⅱ)
上单调递增. (Ⅱ)![]()
【解析】试题分析:(Ⅰ)当![]() 时,
时, ![]() ,求导因式分解可得单调区间;
,求导因式分解可得单调区间;
(2)利用导数将不等式恒成立问题转化为对单调性的讨论,再利用单调性求解参数范围.
试题解析:(Ⅰ)当![]() 时,
时, ![]()
则![]() ,
,
![]()
此时:函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
, ![]() 上单调递增.
上单调递增.
(Ⅱ)依题意有: ![]()
![]() ,
,
令![]() ,
,
得: ![]() ,
,
①当![]() 即
即![]() 时,
时,
函数![]() 在
在![]() 恒成立,
恒成立,
则![]() 在
在![]() 单调递增,
单调递增,
于是![]() ,
,
解得: ![]() ;
;
②当![]() 即
即![]() 时,
时,
函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
于是![]() ,不合题意,
,不合题意,
此时: ![]() ;
;
综上所述:实数![]() 的取值范围是
的取值范围是![]()
点晴:本题主要考查函数单调性,不等式恒成立问题.要求单调性,求导比较导方程的根的大小,解不等式可得单调区间,要证明不等式恒成立问题可转化为构造新函数证明新函数单调,只需要证明其导函数大于等于0(或者恒小于等于0即可),要证明一个不等式,我们可以先根据题意构造新函数,求其值最值即可.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
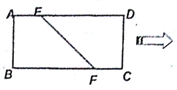
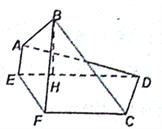
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA-csinC=b(sinA-sinB).
(Ⅰ)求角C的大小;
(Ⅱ)若边长c=4,求△ABC的周长最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=elnx,g(x)=![]() f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)
(1)求函数g(x)的极大值;
(2)求证:1+![]() +
+![]() +…+
+…+![]() >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3+
x3+![]() x2+
x2+![]() x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
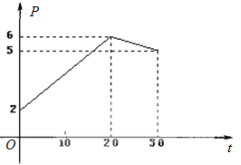
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在图中的两条线段上.
落在图中的两条线段上.
该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如下表所示:
(天)的部分数据如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该股票每股交易价格![]() (元)与时间
(元)与时间![]() (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)根据表中数据,写出日交易量![]() (万股)与时间
(万股)与时间![]() (天)的一次函数关系式;
(天)的一次函数关系式;
(3)用![]() (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出![]() 关于
关于![]() 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com