
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良. 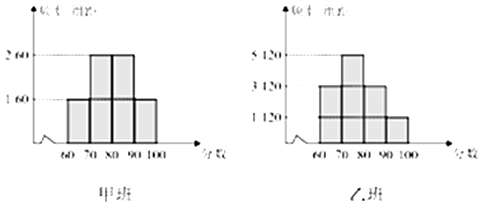
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良 | 优良(人数) | 非优良(人数) | 合计 |
甲 | |||
乙 | |||
合计 |
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率. 下面的临界值表供参考:
P(x2k) | 0.10 | 0.05 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
(以下临界值及公式仅供参考 ![]() ,n=a+b+c+d)
,n=a+b+c+d)
【答案】
(1)解:根据题意,填写2×2列联表如下;
是否优良 班级 | 优良 (人数) | 非优良 (人数) | 合计 |
甲 | 30 | 30 | 60 |
乙 | 20 | 40 | 60 |
合计 | 50 | 70 | 120 |
计算 ![]() ,
,
则有90%的把握认为学生成绩优良与班级有关
(2)解:分层抽样甲班抽取了3人,记作a1,a2,a3,乙班抽取了2人,记作b1,b2,
从中任意抽取2人,有{a1,a2},{a1,a3},{a1,b1},{a1,b2},
{a2,a3},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{b1,b2}10种情形,
其中2人都来自甲班的有3种情形,
则至少有2人来自甲班的概率为P= ![]()
【解析】(1)根据所给数据可得列联表,利用公式计算K2的值,对照临界值即可得结论;(2)利用分层抽样原理与列举法计算基本事件数,求出对应的概率值.


科目:高中数学 来源: 题型:
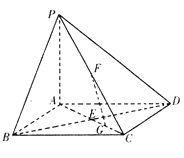
【题目】如图,在底面是正方形的四棱锥![]() 面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:![]() ;
;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(3)当二面角![]() 的大小为
的大小为![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() .
.
(1)求![]() 的值并求函数
的值并求函数![]() 的值域;
的值域;
(2)若关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为
的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
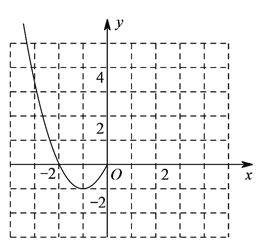
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,请根据图象.
轴左侧的图象,如图所示,请根据图象.
(![]() )写出函数
)写出函数![]() 的增区间.
的增区间.
(![]() )写出函数
)写出函数![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足:对任意的x1 , x2∈(﹣∞,0),有 ![]() ,则( )
,则( )
A.f(﹣4)<f(3)<f(﹣2)
B.f(﹣2)<f(3)<f(﹣4)
C.f(3)<f(﹣2)<f(﹣4)
D.f(﹣4)<f(﹣2)<f(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某城市气象部门的数据中,随机抽取了100天的空气质量指数的监测数据如表:
空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | (300,+∞) |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)在该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t(t取整数)存在如下关系y= ![]() ,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
(2)若在(1)中,当t>300时,y与t的关系拟合于曲线 ![]() ,现已取出了10对样本数据(ti , yi)(i=1,2,3,…,10),且
,现已取出了10对样本数据(ti , yi)(i=1,2,3,…,10),且 ![]() =42500,
=42500, ![]() =500,求拟合曲线方程. (附:线性回归方程
=500,求拟合曲线方程. (附:线性回归方程 ![]() =a+bx中,b=
=a+bx中,b= ![]() ,a=
,a= ![]() ﹣b
﹣b ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com