
设平面向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx+2
=(cosx+2![]() ,s inx),
,s inx),![]() =(sinα,cosα),x∈R.
=(sinα,cosα),x∈R.
(1)若![]() ⊥
⊥![]() ,求cos(2x+2α)的值;
,求cos(2x+2α)的值;
(2)若x∈![]() ,证明
,证明![]() 和
和![]() 不可能平行;
不可能平行;
(3)若α=0,求函数f(x)=![]() ·(
·(![]() -2
-2![]() )的最大值,并求出相应的x的值.
)的最大值,并求出相应的x的值.
解:(1)若![]() ⊥
⊥![]() ,则
,则![]() ·
·![]() =0,
=0,
cosxsinα+sinxcosα=0,sin(x+α)=0,
所以cos(2x+2α)=1-2sin2(x+α)=1.
(2)证明:假设![]() 和
和![]() 平行,则cosxsinx-sinx(cosx+2
平行,则cosxsinx-sinx(cosx+2![]() )=0,
)=0,
即2![]() sinx=0,sinx=0,而x∈
sinx=0,sinx=0,而x∈![]() 时,sinx>0,矛盾.
时,sinx>0,矛盾.
故假设不成立,所以![]() 和
和![]() 不可能平行.
不可能平行.
(3)若α=0,则c=(0,1),则f(x)=![]() ·(
·(![]() -2c)
-2c)
=(cosx,sinx)·(cosx+2![]() ,sinx-2)
,sinx-2)
=cosx(cosx+2![]() )+sinx(sinx-2)
)+sinx(sinx-2)
=1-2sinx+2![]() cosx=1+4sin
cosx=1+4sin![]() ,所以f(x)max=5,此时,x=2kπ-
,所以f(x)max=5,此时,x=2kπ-![]() ,k∈Z.
,k∈Z.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2007年安徽省自主命题高考仿真卷理科数学(二) 题型:013
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设![]() =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an),![]() =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量![]() 与
与![]() 夹角θ的余弦为
夹角θ的余弦为 .当
.当![]() =(1,1,1,1,…,1),
=(1,1,1,1,…,1),![]() =(-1,-1,1,1,…,1)时,cosθ=
=(-1,-1,1,1,…,1)时,cosθ=
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:山东省济宁汶上一中2012届高三12月月考数学理科试题 题型:044
设![]() =(cosα,(λ-1)sinα),
=(cosα,(λ-1)sinα),![]() =(cosβ,sinβ),(λ>0,0<β<
=(cosβ,sinβ),(λ>0,0<β<![]() )是平面上的两个向量,若向量
)是平面上的两个向量,若向量![]() +
+![]() 与
与![]() -
-![]() 互相垂直.
互相垂直.
(Ⅰ)求实数λ的值;
(Ⅱ)若![]() ·
·![]() =
=![]() ,且tanβ=
,且tanβ=![]() ,求tanα的值.
,求tanα的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省盐城市高三上学期期中考数学试卷(解析版) 题型:填空题
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量 ,
, ,当
,当 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________
查看答案和解析>>
科目:高中数学 来源:2014届湖南省衡阳市、八中高一下学期期中数学试卷(解析版) 题型:解答题
(本题满分9分)
设平面上向量 =(cosα,sinα) (0°≤α<360°),
=(cosα,sinα) (0°≤α<360°), =(-
=(- ,
, ).
).
(1)试证:向量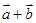 与
与 垂直;
垂直;
(2)当两个向量 与
与 的模相等时,求角α.
的模相等时,求角α.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com