银行按规定每经过一定的时间结算存(贷)款的利息一次,结算后即将利息并入本金,这种计算利息的方法叫做复利.现在有某企业进行技术改造,有两种方案:
甲方案:一次性贷款10万元,第一年便可获得利润1万元,以后每年比上年增加30%的利润;
乙方案:每年贷款1万元,第一年可获得利润1万元,以后每年比前一年多获利5000元.
两种方案的期限都是10年,到期一次行归还本息.若银行贷款利息均以年息10%的复利计算,试比较两个方案哪个获得存利润更多?(计算精确到千元,参考数据:1.110=2.594,1.310=13.796)
【答案】
分析:由题意可知,甲方案中增长利率是定值,所以每年利润数是以1为首项,以1.3为公比的等比数列,再由等比数列的前n项和公式求出10年利润总数;乙方案中每年增长的利润是一定值,所以每年利润数是以1为首项,以0.5为公差的等差数列,再由等差数列的前n项和公式求出10年利润总数,然后比较两种情况的数值.
解答:解:甲方案10年获利润是每年利润数组成的数列的前10项的和:
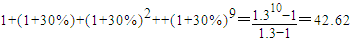
(万元)
到期时银行的本息和为10×(1+10%)
10=10×2.594=25.94(万元)
∴甲方案扣除本息后的净获利为:42.62-25.94≈16.7(万元)
乙方案:逐年获利成等差数列,前10年共获利:
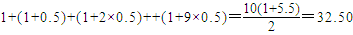
(万元)
贷款的本利和为:
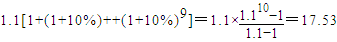
(万元)
∴乙方案扣除本利后的净获利为:32.50-17.53=15.0(万元)
所以,甲方案的获利较多.
点评:数列应用问题主要涉及产品增长率,银行利率,浓度配比,分期付款等问题,解题时建立数列模型,应用数列的相应知识进行求解.要注意审题,理解题中的实际意义,选择合适的模型,将实际问题转化为数列问题.

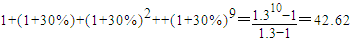 (万元)
(万元)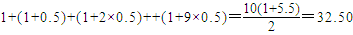 (万元)
(万元)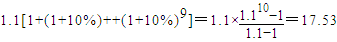 (万元)
(万元)
