
【题目】甲、乙二人独立破译同一密码,甲破译密码的概率为![]() ,乙破译密码的概率为
,乙破译密码的概率为![]() .记事件A:甲破译密码,事件B:乙破译密码.
.记事件A:甲破译密码,事件B:乙破译密码.
(1)求甲、乙二人都破译密码的概率;
(2)求恰有一人破译密码的概率;
(3)小明同学解答“求密码被破译的概率”的过程如下:
解:“密码被破译”也就是“甲、乙二人中至少有一人破译密码”所以随机事件“密码被破译”可以表示为![]() 所以
所以![]()
请指出小明同学错误的原因?并给出正确解答过程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)由相互独立事件概率乘法公式求解即可;
(2)恰有一人破译密码表示为![]() ,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解;
,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解;
(3)小明求解错误的原因是事件![]() 和事件
和事件![]() 不互斥,然后将甲、乙二人中至少有一人破译密码表示为
不互斥,然后将甲、乙二人中至少有一人破译密码表示为![]() ,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解.
,再利用互斥事件概率加法公式和相互独立事件概率乘法公式求解.
(1)由题意可知![]() ,
,![]() ,且事件A,B相互独立,
,且事件A,B相互独立,
事件“甲、乙二人都破译密码”可表示为![]() ,
,
所以![]() ;
;
(2)事件“恰有一人破译密码”可表示为![]() ,且
,且![]() ,
,![]() 互斥
互斥
所以![]()
![]()
(3)小明同学错误在于事件A,B不互斥,而用了互斥事件的概率加法公式
正确解答过程如下
“密码被破译”也就是“甲、乙二人中至少有一人破译密码”
可以表示为![]() ,且
,且![]() ,
,![]() ,
,![]() 两两互斥
两两互斥
所以![]()
![]()


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
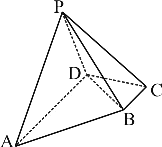
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列结论正确的是( )
A.四面体ABCD每组对棱相互垂直
B.四面体ABCD每个面的面积相等
C.从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°且小于180°
D.连接四面体ABCD每组对棱中点的线段相互垂直平分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取:
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费L(x)(元)与用电量x(度)间的函数关系.若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
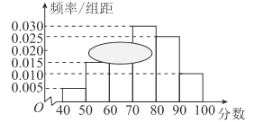
(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com