
分析 分段函数求解得出2x-a=0,x2-3ax+2a2=(x-a)(x-2a),分类分别判断零点,总结出答案.
解答 解:∵y=2x,x<2,0<2x<4,
∴0<a<4时,2x-a=0,有一个解,
a≤0或a≥4,2x-a=0无解
∵x2-3ax+2a2=(x-a)(x-2a),
∴当a∈(0,1)时,
方程x2-3ax+2a2=0在[1,+∞)上无解;
当a∈[1,2)时,
方程x2-3ax+2a2=0在[1,+∞)上有且仅有一个解;
当a∈[2,+∞)时,
方程x2-3ax+2a2=0在x∈[1,+∞)上有且仅有两个解;
综上所述,函数f(x)恰有2个零点,1≤a<2,或a≥4
故答案为:1≤a<2,或a≥4
点评 本题考查了分段函数的性质的应用及分类讨论的思想应用,把问题分解研究的问题,拆开来研究,从多种角度研究问题,分析问题的能力.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
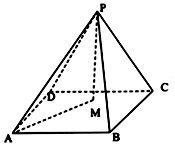 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )| A. | 一个点 | B. | 线段 | C. | 圆 | D. | 圆弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
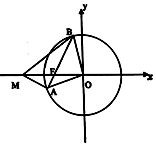 已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.
已知圆O:x2+y2=16及圆内一点F(-3,0),过F任作一条弦AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30万元 | B. | 22.5万元 | C. | 10万元 | D. | 7.5万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com